Table of Contents
Flow around Surface-Mounted Cubical Obstacle
Experiments by Martinuzzi and Tropea
Description
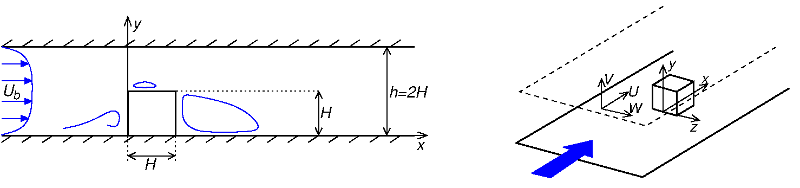
The flow field around a surface-mounted cube has been investigated, using LDA measurement techniques. The experiments were performed in a fully developed channel flow, so that the incoming flow conditions are well-defined. The Reynolds number, based on the height of the channel, is around \(8\times 10^4\), and the geometry and coordinate system are shown schematically in figure 1.
Experimental Apparatus and Techniques
The flow considered here was investigated by means of LDA measurements.
The dimensions of the channel are 390 cm by 60 cm by 5 cm (\(l \times w \times h\)). The cube, of height \(H=h/2\), was placed with its leading edge 52 channel heights downstream of the inlet. The boundary-layer was tripped at the inlet in order to obtain fully-developed conditions at least 5 channel heights upstream of the front face of the cube.
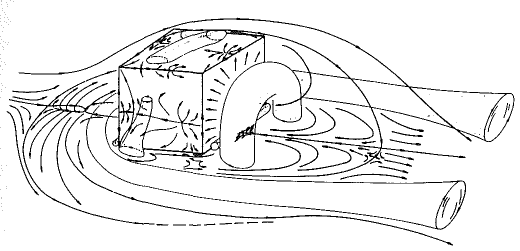
Flow visualisation and surface pressure measurements are also reported in Martinuzzi & Tropea (1993). A sketch illustrating the flow structures identified is shown in figure 2.
Available Measurements
Measurements available include profiles across the channel height at a selection of locations (both on, and off, the flow centreline) of:
- Mean velocities, \(U\), \(V\), \(W\)
- Reynolds stresses, \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\), \(\overline{uv}\), \(\overline{uw}\)
- Third and fourth order moments
Sample plots of selected quantities are available.
The plots in figure 3 and figure 4 indicate the locations at which profiles are provided.
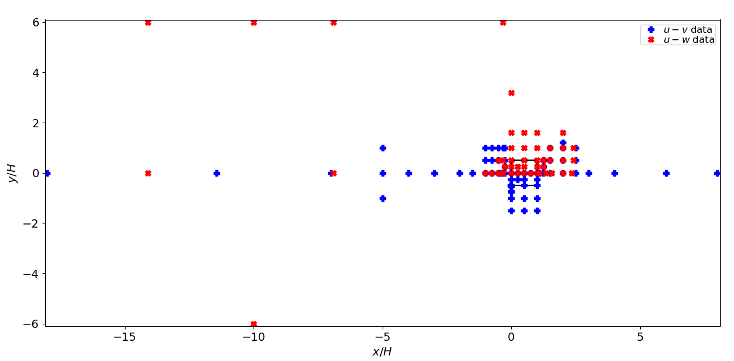 Fig. 3: Locations of measured profiles
Fig. 3: Locations of measured profiles
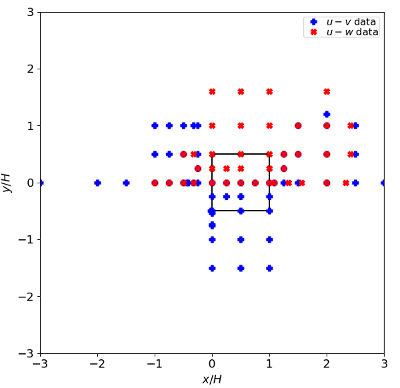 Fig. 4: Detail of measured profile locations around the cube
Fig. 4: Detail of measured profile locations around the cube
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt contains some description of the data files.
References
- Hussain, H.J., Martinuzzi, R.J. (1996). Energy balance for turbulent flow around a surface mounted cube placed in a channel. Phys. Fluids, Vol. 8, pp. 764-780.
- Martinuzzi, R., Tropea, C. (1993). The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. Journal of Fluid Engineering, Vol. 115, pp. 85-92.
- Martinuzzi, R., Prud'homme, M. (1993). Higher-order correlations for the turbulent flow around a surface-mounted cube placed in a channel. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
- Martinuzzi, R., Melling, A., Tropea, C. (1993). Reynolds stress field for the turbulent flow around a surface-mounted cube placed in a channel. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
- Murakami, S., Mochida, A., Ooka, R. (1993). Numerical simulation of flowfield over surface-mounted cube with various second-moment closure models. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
Indexed data:
| case041 (dbcase, semi_confined_flow, flow_around_body) | |
|---|---|
| case | 041 |
| title | Flow Around Surface-Mounted Cubical Obstacle |
| author | Martinuzzi, Tropea |
| year | 1993 |
| type | EXP |
| flow_tag | 3d, surface_mounted_body |