Table of Contents
Swirling Mixing Layer
Experiments by Mehta, Wood and Clausen
Description
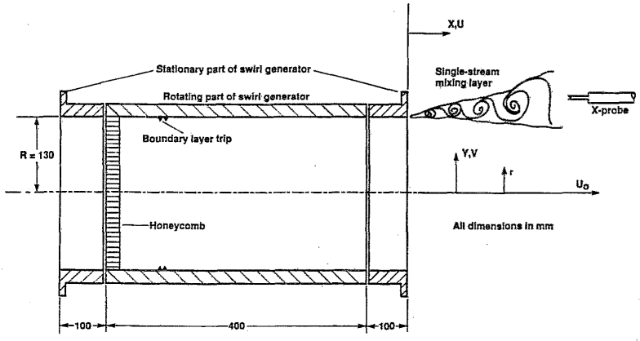
An experimental study has been conducted to investigate the effects of swirl on the streamwise development of an axisymmetric turbulent mixing layer. The flow geometry is shown in figure 1. The initial boundary layer was tripped well upstream of the lip, and all three mean velocities and the six independent components of the Reynolds stress tensor were measured using a rotatable cross-wire probe for three swirl numbers (\(S=0\), \(0.2\), and \(0.4\)).
- \(S = W_{max}/U_o = 0\), \(0.2\) and \(0.4\)
- \(Re_{exit} =U_oR/\nu = 130,000\)
Experimental Details
The experiments were conducted in a standard open-circuit blower wind tunnel connected to the upstream end of a swirl generator. Details of the swirl generator, together with the co-ordinate system employed, are shown in figure 1.
The swirl generator, of internal radius \(R = 130\) mm, consisted of an aluminium honeycomb at the start of the rotating section followed by two rows of Dymo tape attached to the pipe wall. The honeycomb was about 25 mm long with a cell diameter of 3.2 mm and wall thickness of 0.025 mm, giving an open-area ratio of about 97%. The two rows of Dymo tape were installed 60 mm downstream of the honeycomb in order to trip the boundary layer. Each segment of the tape was 12.7 mm wide and was inscribed with a continuous succession of “V's” with the “legs” pointing downstream and a wavelength of about 6 mm. The apices on the two rows were staggered by half of a wavelength. The measurements were made in a vertical plane through the axisymmetric mixing layer that originated from the downstream end of the 100 mm long stationary section.
Measurements were obtained at six to eight streamwise locations, between \(X/R = 0.19\) to \(4.62\) (\(X = 25\) to \(600\) mm), at an axial exit velocity of about 15 m/s. Three rotational speeds of the swirl generator were investigated, \(\Omega = 0\), \(28.8\), and \(57.6\) rad/s (0, 275, and 550 rpm). These rotational speeds gave swirl numbers \(S = 0\), \(0.2\), and \(0.4\). The swirl number here is defined as \(S = W_{max}/U_o\), where \(W\) is the mean circumferential velocity and \(U_o\) is the mean centerline free-stream velocity. In terms of the more conventional definition for swirl number \(G_{\theta}/(RG_x)\), where \(G_{\theta}\) is the angular momentum flux and \(G_x\) the axial momentum flux, the values are 0, 0.1, and 0.2. The standard deviation of the swirl number calculated at the various streamwise locations was about 5% for both rotation rates.
The turbulence measurements were obtained using a DANTEC 55P5 1 X probe mounted on an automated traverse system. The sensing elements on the X probe were comprised of home-made tungsten wires. These had a diameter of 5\(\mu\)m and an active portion of 1.2 mm that was isolated from the prongs by copper-plated stubs of 20\(\mu\)mm diam. A single-wire probe was used to measure the conventional \(U\) and \(W\) using similar techniques to those used for the X probe.
The active length and other dimensions of the single-wire were the same as for the X wires, as were the anemometers and data acquisition. At each radius, the probe was yawed to find \(Q\), the “total” velocity defined by \(Q^2 = U^2 + W^2\). This was done in 5o steps, the large step size being justified by the nearly flat yaw response of the X probe at small angles. The probe was then yawed by an additional 30o - 40o to find \(W/U\) using the more sensitive yaw response at large angles.
The X probe measurements were obtained at each radius after rotating the probe by approximately \(\beta = \tan^{-1}(W/U)\) so that it was aligned with the local flow direction. This procedure minimised errors due to contamination by velocities transverse to the plane of the wires.
Measurements were obtained in four planes by rotating the plane of the wires about the probe axis.
Measurement Errors
The overall measurement accuracy of the Reynolds stresses was estimated at around 10%.
Available measurements
Data available includes:
- Profiles of mean \(U\) velocity, flow angle and Reynolds stresses at selected streamwise locations (\(X/=0.19\), \(0.38\), \(0.77\), \(1.54\), \(2.31\), \(3.08\) and \(4.62\) for the \(S=0\) case; (\(X/=0.19\), \(0.38\), \(0.77\), \(1.54\), \(2.31\) and \(3.08\) for the \(S=0.2\) and \(0.4\) cases)
- Streamwise development of the mixing layer width for the three cases
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt gives details of the file naming convention and data format.
| \(S=0\) Case | \(S=0.2\) Case | \(S=0.4\) Case | |
|---|---|---|---|
| Mixing layer width development | s0_delta.dat | s2_delta.dat | s4_delta.dat |
| u-v plane data at \(X/R=0.19\) | s0_x019v.dat | s2_x019v.dat | s4_x019v.dat |
| u-w plane data at \(X/R=0.19\) | s0_x019w.dat | s2_x019w.dat | s4_x019w.dat |
| u-v plane data at \(X/R=0.38\) | s0_x038v.dat | s2_x038v.dat | s4_x038v.dat |
| u-w plane data at \(X/R=0.38\) | s0_x038w.dat | s2_x038w.dat | s4_x038w.dat |
| u-v plane data at \(X/R=0.77\) | s0_x077v.dat | s2_x077v.dat | s4_x077v.dat |
| u-w plane data at \(X/R=0.77\) | s0_x077w.dat | s2_x077w.dat | s4_x077w.dat |
| u-v plane data at \(X/R=1.54\) | s0_x154v.dat | s2_x154v.dat | s4_x154v.dat |
| u-w plane data at \(X/R=1.54\) | s0_x154w.dat | s2_x154w.dat | s4_x154w.dat |
| u-v plane data at \(X/R=2.31\) | s0_x231v.dat | s2_x231v.dat | s4_x231v.dat |
| u-w plane data at \(X/R=2.31\) | s0_x231w.dat | s2_x231w.dat | s4_x231w.dat |
| u-v plane data at \(X/R=3.08\) | s0_x308v.dat | s2_x308v.dat | s4_x308v.dat |
| u-w plane data at \(X/R=3.08\) | s0_x308w.dat | s2_x308w.dat | s4_x308w.dat |
| u-v plane data at \(X/R=4.62\) | s0_x462v.dat | ||
| u-w plane data at \(X/R=4.62\) | s0_x462w.dat |
References
- Mehta, R.D., Wood, D.H., Clausen, P.D. (1991). Some effects of swirl on turbulent mixing layer development. Phys. Fluids A, Vol. 3, pp. 2716-2724.
- Wood, D.H., Mehta, R.D., Koh, S.G. (1992). Structure of a swirling turbulent mixing layer. Experimental Thermal and Fluid Science, Vol. 5, pp. 196-202.
Indexed data:
| case059 (dbcase, free_flow) | |
|---|---|
| case | 059 |
| title | Swirling mixing layer |
| author | Mehta, Wood, Clausen |
| year | 1991 |
| type | EXP |
| flow_tag | axisymmetric, mixing_layer, swirl |