Table of Contents
Torque Scaling in Taylor-Couette Flow
Experiments by Merbold, Fischer and Egbers
Description
The turbulent flow between two concentric cylinders of radii \(R_1\), \(R_2\) and length \(L\), which are rotating independently with the angular velocities \(\Omega_1\) and \(\Omega_2\), is investigated. Important parameters of this geometry are the radius ratio \(\eta = R_2/R_1\), the aspect ratio \(\Gamma = L/(R_2 - R_1) = L/d\) and the ratio of rotation rates \(\mu = \Omega_2/\Omega_1\). To indicate the flow in the gap, one can derive two Reynolds numbers related to the inner and outer rotation \(Re_{1,2} = R_{1,2} \Omega_{1,2} d/\nu\), with the kinematic viscosity \(\nu\) of the fluid. The angular velocity of the fluid \(\omega\) across the gap is measured by Particle Image Velocity and LASER Doppler Anemometry for different rotation rates of the inner and outer cylinder. The aim is to analyse the angular velocities \(\omega\) as well as the torque \(T\) acting on the inner cylinder for the case when only the outer cylinder rotates.
Experimental details
Experimental Apparatus
In our initial investigations we use the Taylor-Couette apparatus as illustrated in figure 1. The outer cylinder is made out of high precision duran glass with an inner radius of \(R_2 = 70 \pm 0.02\) mm. The inner cylinder is made of black anodised aluminium with radius \(R_1 = 35\) mm, resulting in a radius ratio \(\eta = 0.5\). The end plates are adjustable up to a length of 735 mm. In the present experiments we choose this to be fixed at L = 700 mm, resulting in an aspect ratio of \(\Gamma = 20\). The inner cylinder is able to rotate up to a rotation rate of \(n_1 = 80\) Hz, the outer one up to \(n_2 = 40\) Hz. In addition, the two end plates are rotatable independently with the same speed as the cylinders or in between. As working fluid, we use Wacker silicone oil AK065 with a kinematic viscosity of \(\nu = 0.65\times 10^{-6}\) m2/s. Therewith we reach Reynolds numbers of the inner and outer rotation of \(Re_{1,2}= 9.5\times 10^5\). The temperature of this experiment is controlled through a water bath surrounding the outer cylinder. This allows to control the heat, which is produced by the bearings, sealings and inside the experiment. The inner cylinder is subdivided into three parts of lengths 99.4 mm, 500 mm and 99.4 mm with a gap of 0.6 mm separating the parts [see <cas89-geom1>, right]. Both end parts are directly connected to the axial drifting shaft. The middle part is mounted rotatable against the shafts by two strain gauges. If the inner cylinder is driven by the 1.1 kW motor, the inner part can distort slightly with respect to the shaft. The torque working on the middle part of the inner cylinder is quantifiable by the strain gauges. The objective of the separation is to reduce the end effects of the solid end plates on the torque measurement. Slip rings transfer the signal out of the rotating cylinder into the convertor WZSG of the company Wachendorff sampling at a rate of 100 Hz. Fluid flow measurements by means of Particle Image Velocimetry (PIV) and LASER Doppler Anemometry (LDA) are done through the transparent water bath tank and outer cylinder.
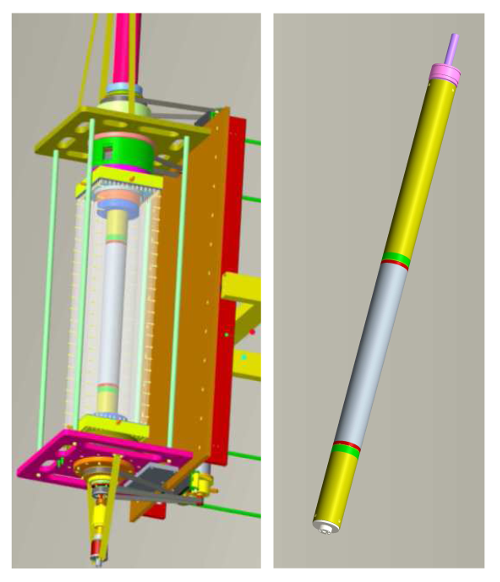 Fig. 1: Left: Drawing of the Taylor-Couette system with surrounding
water bath. Right: The inner cylinder is separated into three sections. The
middle section measures the torque. The upper and lower sections are beared
inside the end plates as shown in the left.
Fig. 1: Left: Drawing of the Taylor-Couette system with surrounding
water bath. Right: The inner cylinder is separated into three sections. The
middle section measures the torque. The upper and lower sections are beared
inside the end plates as shown in the left.
In addition to this experiment another Taylor-Couette experiment with the same geometry as the first was also built [see figure 2]. Here the end plates are transparent, but attached to the outer cylinder. This gave the possibility to measure the azimuthal and radial velocity simultaneously from above without light refraction at the cylindrical surface. The Reynolds numbers of this experiment were in the range of 104, due to the gearings and driving motors.
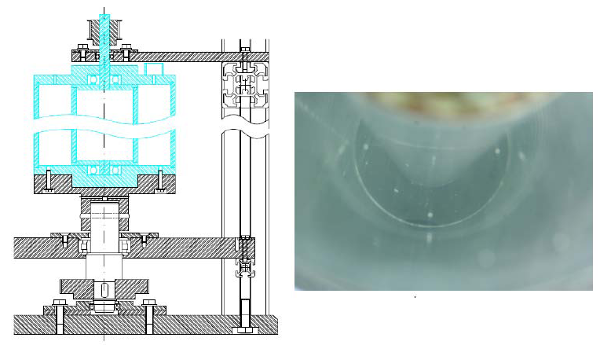 Fig. 2: Left: Drawing of the transparent Taylor-Couette system. Right: View through the
transparent upper plate into the measurement volume.
Fig. 2: Left: Drawing of the transparent Taylor-Couette system. Right: View through the
transparent upper plate into the measurement volume.
Angular velocity profiles and torque measurements
Inside the second described Taylor-Couette system with transparent end plates, a PIV measurement system was applied. The lightsheet illuminated an azimuthal-radial plane in the mid-hight of the experiment, and the plane through the upper end was observed. The field of view was about more than one fifth of the whole gap. The measured two dimensional, time averaged, Cartesian flow field was interpolated into a cylindrical coordinate system. The tables with angular velocities are averaged over \(2\pi /5\) for different radii. With the second Taylor-Couette apparatus the torque acting on the inner cylinder, \(T\), was measured. This is of great interest to quantify the angular momentum transport \(J_{\omega} = T / (2 \pi L \rho)\) as well as to give informations about the energy dissipation rate \(\varepsilon_w\) at the inner cylinder.
Available Data
Data available includes:
- Profiles of the mean angular velocity across the annular gap for a variety of combinations of inner and outer cylinder rotation rates
- Non-dimensional torque (\(G = T / (2 \pi L \rho \nu^2\))) for a range of outer cylinder rotation rates (with the inner cylinder at rest)
Sample plots of selected quantities are available.
The data files can be downloaded as compressed archives, or individually from the tables below (data files are available as both plain text file and Excel spreadsheet).
The table below shows the angular velocity for different pairs of inner and outer rotation Reynolds numbers \(Re_{1,2}\). In Merbold et al (2011) these are compared with the theoretical Couette flow profile
\[ \omega_{stationary}(r) = a + b/r^2 \]
with \(a\) and \(b\) two geometrical factors, \(a = ( R_2^2 \Omega_2 - R_1^2 \Omega_1)/(R_2^2 - R_1^2)\) and \(b = R_1^2 R_2^2 ( \Omega_1 - \Omega_2 ) / ( R_2^2 - R_1^2) \).
| \(Re_1\) | \(Re_2\) | File | Notes | |
|---|---|---|---|---|
| Case A | \(0\) | \(-7.7\times 10^3\) | angular_velocities_a.dat angular_velocities_a.xls | Linear stable flow |
| Case B | \(0\) | \(-1.5\times 10^4\) | angular_velocities_b.dat angular_velocities_b.xls | Linear stable flow |
| Case C | \(2.5\times 10^4\) | \(0\) | angular_velocities_c.dat angular_velocities_c.xls | Linear unstable flow |
| Case D | \(2.5\times 10^4\) | \(1.26\times 10^4\) | angular_velocities_d.dat angular_velocities_d.xls | Cylinders co-rotating at the Rayleigh-criterion |
| Case E | \(2.5\times 10^4\) | \(-4.0\times 10^4\) | angular_velocities_e.dat angular_velocities_e.xls | Linear unstable flow, counter-rotation |
| Case F | \(4.0\times 10^4\) | \(-4.0\times 10^4\) | angular_velocities_f.dat angular_velocities_f.xls | Linear unstable flow, counter-rotation |
| Case G | \(6.0\times 10^4\) | \(3.1\times 10^4\) | angular_velocities_g.dat angular_velocities_g.xls | Linear stable flow, co-rotation |
The file below contains profiles of the dimensionless time averaged angular velocity \(\omega / \Omega_1\) for a range of Reynolds numbers of the inner cylinder rotation, \(Re_1\), with the outer cylinder at rest.
| File | Notes |
|---|---|
| dimensionless_angular_velocity.dat dimensionless_angular_velocity.xls | Profiles for \(Re_1 = 9376\), \(13885\), \(20902\), \(26449\), \(33202\), \(42390\), \(51445\), \(60877\) |
The file below contains the dimensionless torque \(G = T/(2 \pi L \rho \nu^2\)) for a range of outer rotation Reynolds numbers, \(Re_2\), while inner cylinder is at rest.
| File | Notes |
|---|---|
| dimensionless_torque.dat dimensionless_torque.xls | Dimensionless torque for \(35524 \le Re_2 \le 78942\) |
References
- Merbold, S., Fisher, S., Egbers, C. (2011). Torque scaling in Taylor-Couette flow - an experimental investigation. Journal of Physics: Conference Series, Vol. 318, p. 082017.
Acknowledgements
The authors gratefully acknowledge the financial support for their research work from the German Science Foundation (DFG), Germany, FOR 1182 - DFG Research Group: Transport and Coherent Structures in Turbulent Rayleigh-Bénard, Taylor-Couette and Pipe Flows.
Indexed data:
| case089 (dbcase, confined_flow) | |
|---|---|
| case | 089 |
| title | Torque Scaling in Taylor-Couette Flow |
| author | Merbold, Fischer, Egbers |
| year | 2011 |
| type | EXP |
| flow_tag | axisymmetric |