Measurements and Numerical Determination in Differentially Rotating Wide Gap Taylor-Couette Flow
Experiments and DNS by Merbold, Brauckmann and Egbers
Description
Turbulent Taylor-Couette flow with independently rotating cylinders and radius ratio \(\eta = R_2 / R_1 = 0.5\) has been investigated experimentally and numerically. Other important parameters of this geometry are the aspect ratio, \(\Gamma = L / (R_2 - R_1) = L / d\) (\(L\) being the length of the cylinders, and \(d\) the gap width) and the ratio of rotation rates, \(\mu = \Omega_2/ \Omega_1\).
To characterise the flow in the gap, one can derive two Reynolds numbers related to the inner and outer rotation \(Re_{1,2} = R_{1,2} \Omega_{1,2} d /\nu\), with \(\nu\) the kinematic viscosity of the fluid. In analogy to other shear flows, a shear Reynolds number is defined as \(Re_S = 2 |Re_1 - \eta Re_2 | / (1+\eta) = 2 R_1 R_2 d |\Omega_2 - \Omega_1| / (R_1+R_2) \nu\).
The torque acting on the inner wall was measured to analyze the transverse current of azimuthal motion \(J_{\omega}\). The scaling of the torque with shear Reynolds number was determined for the outer cylinder at rest. The transverse current of azimuthal motion \(J_{\omega}\) is constant over all radii, with \(J_{\omega} = r^3(\langle u_r \omega\rangle_{A,t} - \nu \partial_t \langle \omega \rangle_{A,t})\), where the brackets \(\langle \rangle_{A,t}\) denote a mean over a cylindrical surface at radius \(r\) and over time. The cylinders are impermeable so that the radial velocity \(u_r\) and the first term of the previous relation are equal to zero at the boundaries (\(u_r(r = R_1, R_2) = 0\)). At these radial positions the second term is proportional to the torque \(T\) that the fluid experiences at the boundary. Hence, measuring the dimensionless torque \(G = T / (2 \pi L \rho \nu^2)\) at the rotating inner and outer cylinder corresponds to measuring the current \(J_{\omega} = \nu^2 G\).
Corresponding to the heat transport Nusselt number in Rayleigh-Bénard flow, one can define a quasi-Nusselt number of Taylor-Couette flow \(Nu_{\omega} = G / G_{lam}\), where \(G_{lam} = R_1R_2Re_Sd^{-2}\) is the dimensional torque of the analytical Couette solution. For constant shear Reynolds number various ratios of angular velocities have been investigated, and torque maximum for counter-rotating cylinders found that deviates from the predictions suggested by van Gils et al. (2011). Direct comparison between the experiment and numerical simulations shows a good agreement in the torques.
Experimental details
The experimental investigations were carried out in a Taylor-Couette apparatus surrounded by a water bath box as shown in figure 1. The water bath box and the outer cylinder are made of acrylic glass, the inner cylinder is made of black anodised aluminium. The system radii are \(R_1 = 35 \pm 0.02\) mm and \(R_2 = 70 \pm 0.2\) mm. The end plates were adjusted to fix the system length to 700 +/- 0.1 mm. This gives a radius ratio \(\eta = 0.5\) and an aspect ratio \(\Gamma = 20\). The inner cylinder can be driven up to a rotation rate of 84.5 +/- 0.05 Hz and the outer cylinder up to 12.2 +/- 0.05 Hz. Both end plates can rotate independently, but were kept stationary for this investigation. As working fluid, different silicone oils with kinematic viscosities of \(\nu = 0.65 \times 10^{-6}\) m2/s were used, allowing shear Reynolds numbers of \(10^3 \le Re_S \le 10^6\) to be attained. The temperature of the experiment was controlled to an accuracy of 0.2 K using the water bath. Velocity measurements by means of Particle Image Velocity (PIV) and Laser Doppler Anemometry (LDA) were performed through the transparent water bath tank and outer cylinder (for more details, see Merbold et al., 2013).
 Fig. 1: Drawing and image of the Taylor-Couette system with surrounding water bath. The inner cylinder is separated into three sections. The middle section measures the torque. The upper and lower sections are pivoted inside the end plates.
Fig. 1: Drawing and image of the Taylor-Couette system with surrounding water bath. The inner cylinder is separated into three sections. The middle section measures the torque. The upper and lower sections are pivoted inside the end plates.
The transverse current \(J_{\omega}\) is determined by measuring the torque acting on the inner cylinder as a function of the flow parameters (\(Re_S\), \(\mu\), \(\eta = 0.5\), \(\Gamma = 20\)). The inner cylinder was subdivided into three segments with lengths 99.4 mm, 500 mm and 99.4 mm, and a gap of 0.6 mm separated the segments in a similar way as in other Taylor-Couette set-ups (see figure 1). Only the middle part measures the torque, via two strain gauges mounted inside the cylinder. The objective of the separation is to reduce the end effects of the solid end plates on the torque measurements. Slip rings transfer the signal, and the time series (100 Hz, 60 s) do not show any oscillations or other particular features and fit very well to a Gaussian distribution. The level of standard deviation to mean of the signal is evaluated to be less than 10-2. This torque measurement allowed the transverse \(J_{\omega}\) at the inner boundary to be quantified. With this device it was possible to find the variation of the radial transport of the flow with the input parameters.
Available Data
Data available consist of the measured non-dimensional torque, and resulting quasi-Nusselt number, for a range of rotation ratios, \(\mu\), and shear Reynolds numbers, \(Re_s\).
Sample plots of selected quantities are available.
The data files can be downloaded as compressed archives, or a single plain text file.
| Measured values | tcnu-data.dat |
Discussion of Results
The measured quasi-Nusselt numbers, \(Nu_{\omega} = G / G_{lam}\), are shown in figure 2 for different flow configurations. The classical case where the outer cylinder is at rest (\(\mu = 0\)) is indicated in black. The region of co-rotation is distinguished by the Rayleigh stability criterion \(\mu = \eta^2\), while counter-rotation is distinguished by \(\mu = -0.2\), where the observed maximum in torque is approximately located for the experiments. The scaling of the dimensionless torque with shear Reynolds number \(G \propto Re_S^{\alpha}\) is calculated using \(\mu = 0\) data. Here, one can observe two regimes with scaling exponent of \(\alpha = 1.62 \pm 0.04\) for shear Reynolds numbers \(3 \times 10^3 \le Re_S \le 8 \times 10^4\). For shear Reynolds numbers \(10^5 \le Re_S \le 10^6\) a scaling coefficient of \(\alpha = 1.78 \pm 0.3\) is found, similar to the Twente experiment (\(\alpha = 1.78 \pm 0.06\)). Hence, the \(Re_S\) dependence of the exponent becomes important.
The dependence on \(Re_s\) is also shown in imgref cas92-res1>(b), calculated using a sliding least square fit over different ranges of \(\Delta (\log_{10}Re_S)=\Delta_{10}\). For lower shear Reynolds numbers (\(Re_S \le 8 \times 10^4\)) the fluctuations of the exponent are strong, which is reflected in the correlation coefficient of \(R = 0.97\) for \(\Delta_{10} = 0.2\). For a larger regression interval this becomes less important and \(R\) exceeds 0.99. At high shear Reynolds numbers (\(Re_S > 10^5\)) the local exponent calculated using the largest interval differs from the other two local exponents, which coincide. Here, the correlation coefficient for \(\Delta_{10} =1\) decreases. The calculated exponent in this regime does not appear to be correct any more, while for \(\Delta_{10} = 0.2\) and \(0.6\) the correlation coefficient becomes \(R > 0.995\). Hence the calculation using different intervals influences the interpretation of the scaling exponent.
It can be concluded that the scaling exponent calculated using \(\Delta_{10} = 0.6\) is closest to the real behaviour over the full range of shear Reynolds numbers. The scaling exponent for shear Reynolds numbers \(Re_S > 6 \times 10^5\) seems to tend to a constant value of about \(\alpha = 1.75 \pm 0.05\) for \(\eta = 0.5\) which compares well with the exponent of 1.78 +/- 0.06 by van Gils et al. (2012). Thus, keeping the relatively high uncertainty of this coefficient in mind, the scaling exponent seems not to depend on the curvature of the Taylor-Couette system for high \(Re_S\).
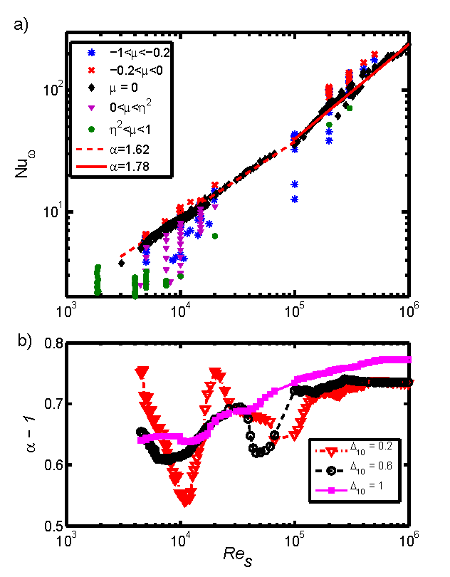 Fig. 2: a) The dependency of the quasi-Nusselt number \(Nu_{\omega} = G/G_{lam}\) on the shear Reynolds number \(Re_S\) over the whole range of measurements. b) Local exponent for the quasi-Nusselt number vs. the shear Reynolds number, calculated from torque measurements for rotation ratio of zero using a sliding least square fit.
Fig. 2: a) The dependency of the quasi-Nusselt number \(Nu_{\omega} = G/G_{lam}\) on the shear Reynolds number \(Re_S\) over the whole range of measurements. b) Local exponent for the quasi-Nusselt number vs. the shear Reynolds number, calculated from torque measurements for rotation ratio of zero using a sliding least square fit.
The experimental results have also been compared to direct numerical simulations for radius ratio \(\eta = 0.5\) and \(\Gamma = 2\) using a Fourier-Chebyshev spectral code with periodic boundary conditions in the axial direction (Merbold et al., 2013). These computations reached up to shear Reynolds number \(Re_S = 2 \times 10^4\) and satisfied three convergence criteria as explained in a study for \(\eta = 0.71\) by Brauckmann and Eckhardt (2012). For \(Re_S = 10^4\) and \(Re_S = 2 \times 10^4\) only one third of the domain did not bias the torque computation. In the lower Reynolds number regime (\(10^3 \le Re_S \le 2 \times 10^4\) ) it was possible to directly compare the measured torques with calculations from direct numerical simulations with the same \(\eta\) but different \(\Gamma = 2\). Torques for three shear Reynolds numbers \(Re_S / 10^3 = 5.0\), \(10\), \(20\) and different ratios of angular velocities, \(\mu\), are compared in figure 3, where the DNS results are indicated by triangles and the measured torques for two different fluids by circles and crosses.
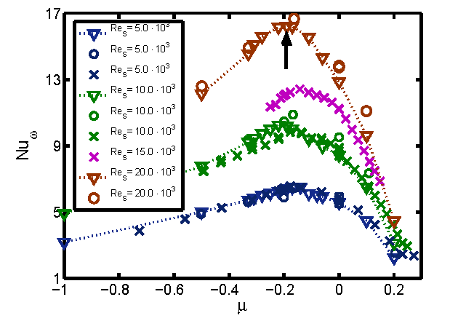 Fig. 3: The dependency of the quasi-Nusselt number on the ratio of rotation rates for constant shear Reynolds numbers. The circles represent experimental torque data for silicon oil with viscosity 8.41E-6 m^2/s, the crosses represent measurements for viscosity 22.81E-6 m^2/s, and the triangles the DNS. Dotted lines serve as guide to the eye, the black arrow indicates the maximum at rotation ratio of -0.2.
Fig. 3: The dependency of the quasi-Nusselt number on the ratio of rotation rates for constant shear Reynolds numbers. The circles represent experimental torque data for silicon oil with viscosity 8.41E-6 m^2/s, the crosses represent measurements for viscosity 22.81E-6 m^2/s, and the triangles the DNS. Dotted lines serve as guide to the eye, the black arrow indicates the maximum at rotation ratio of -0.2.
The numerical and experimental studies show a good agreement with each other in the Rayleigh-unstable regime, with the relative deviation not exceeding 4% for counter-rotating cylinders. Consequently, the restricted numerical domain (\(\Gamma = 2\) and only one third in azimuthal direction) does appear to contain the essential turbulent characteristics to feature the same transport behaviour. The deviation between the numerical and the experimental torques at \(Re_S = 10^4\) for counter-rotation \(\mu < -0.18\) are likely due to different wavelengths of Taylor vortices. The numerical domain selects a wavelength of \(2d\), while the experiment is not able to reproduce this wavelength for these rates. The wavelength became \(2.22d\) for \(\mu < -0.18\) while for angular velocity ratios of \(\mu > -0.18\) the experiments give a wavelength of \(2d\). The influence of different wavelengths has been discussed already by Lathrop et al. (1992) and Lewis and Swinney (1999) and recently in a numerical study (Brauckmann and Eckhardt, 2012).
Obviously, the torque in the both the experimental and numerical studies is maximal at a rotation ratio of \(\mu_{max} = -0.2\) for a wide range of shear Reynolds numbers. Furthermore, the torque measurements for \(10^5 \le Re_S \le 5 \times 10^5\) in figure 4, where no numerical calculations were possible, show that the maximum remains located at \(\mu_{max} = -0.2 \pm 0.02\) for all shear Reynolds numbers in this investigation. In contrast, van Gils et al. (2012), using the bisection of the unstable parameter regime, suggested that the maximum is located at \(\mu_{bis} = -0.31\) for \(\eta = 0.5\). Thus the angle bisector does not coincide with the torque maximum for Taylor-Couette with radius ratio \(\eta = 0.5\).
For Reynolds numbers \(Re_S = 2\times 10^5\) and \(3\times 10^5\) one observes two branches for the torque in the range of \(-1 \le \mu \le -0.1\) in figure 4. These two branches are not failures during the measurement procedure, since they are reproducible. They result from the behaviour of the flow. This suggests that the flow structures changes between different turbulent flow states existing in this parameter regime. When the cylinders are rotating faster than 10 Hz, as they do there, it is nontrivial to observe two different flows. Therefore, visualization of these structures using cameras with high frequency capturing ability should be performed in the future.
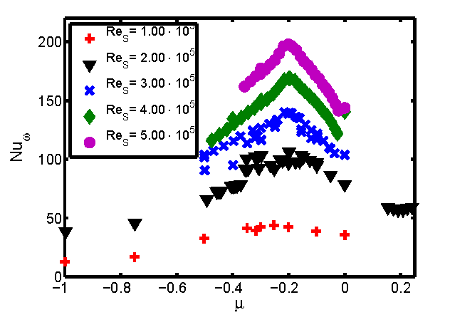 Fig. 4: The dependency of the quasi-Nusselt number on the ratio of rotation rates for constant shear Reynolds numbers
Fig. 4: The dependency of the quasi-Nusselt number on the ratio of rotation rates for constant shear Reynolds numbers
Using the previously described torque data the dependence of \(\mu_{max}\) on \(Re_S\) can be examined. The comparison of the present experimentally-determined \(\mu_{max}\) with the conjectured prediction for the maximum by van Gils et al. (2012) using the bisection of the instable flow regime (\(\mu_{bis} = -0.31\) at \(\eta = 0.5\), is shown in figure 4. The maximum \(\mu_{max\}\) does not follow the trend of the angle bisector with \(Re_S\) and remains at \(\mu_{max\} \approx -0.2\), except for the smallest \(Re_S = 5 \times 10^3\) where \(\mu_{max}\) slightly increases towards less counter-rotation. This is reminiscent of the shift with \(Re_S\) of the torque maximum recently observed for \(\eta = 0.71\) (Esser and Grossmann, 1996).
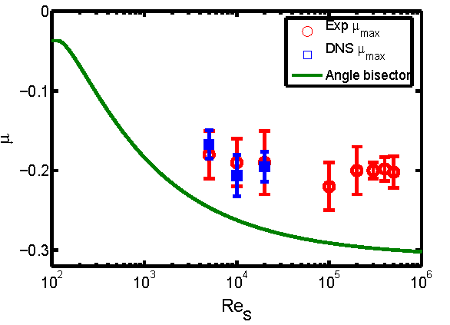 Fig. 5: Ratio of angular velocities of maximal torque vs. the shear Reynolds number from experimental measurement (circles) and numerical simulations (squares). The solid line shows the rotation ratio along the angle bisector line by van Gils et al. (2012) and is calculated using the Esser and Grossmann (1996) stability calculations for viscous fluids.
Fig. 5: Ratio of angular velocities of maximal torque vs. the shear Reynolds number from experimental measurement (circles) and numerical simulations (squares). The solid line shows the rotation ratio along the angle bisector line by van Gils et al. (2012) and is calculated using the Esser and Grossmann (1996) stability calculations for viscous fluids.
References
- Merbold, S., Brauckmann, H.J., Egbers, C. (2013). Torque and numerical determination in differentially rotating wide gap Taylor-Couette flow. Phys. Rev. E, Vol. 87, p. 023014.
- van Gils, D.P.M., Huisman, S., Grossmann, S., Sun, C., Lohse, D. (2012). Optimal Taylor-Couette turbulence. J. Fluid Mech., Vol. 706, p. 118.
- Lathrop, D.P., Fineberg, J., Swinney, H.L. (1992). Transition to shear-driven turbulence in Couette-Taylor flow. Phys. Rev. A, Vol. 46, p. 6390.
- Lewis, G., Swinney, H. (1999). Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette-Taylor flow. Phys. Rev. E, Vol. 59, p. 5457.
- Brauckmann, H.J., Eckhardt, B. (2012). Direct Numerical Simulations of Local and Global Torque in Taylor-Couette Flow up to Re=30,000. J. Fluid Mech., Vol. 718, pp. 398-427.
- Esser, A., Grossmann, S. (1996). Analytic expression for Taylor-Couette stability boundary. Phys. Fluids, Vol. 8, p. 1814.
Acknowledgements
The authors gratefully acknowledge the financial support for their research work from the German Science Foundation (DFG), Germany, FOR 1182 - DFG Research Group: Transport and Coherent Structures in Turbulent Rayleigh-Bénard, Taylor-Couette and Pipe Flows.
Indexed data:
| case092 (dbcase, confined_flow) | |
|---|---|
| case | 092 |
| title | Measurements and numerical determination in differentially rotating wide gap Taylor-Couette flow |
| author | Merbold, Brauckmann, Egbers |
| year | 2013 |
| type | EXP |
| flow_tag | axisymmetric |