Table of Contents
Laterally Strained Boundary Layers
Experiments by Pompeo, Bettelini, Thomann
Description
Turbulent boundary layers on a flat surface laterally strained by converging or diverging walls. 3D flow with constant temperature.
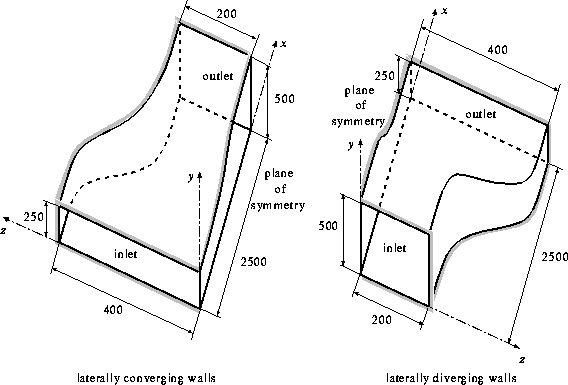
Geometry of the Computational Domain
The cross-section of the duct remains nearly constant along the \(x\) axis for both the laterally converging and diverging wall geometry configurations. The geometry of the duct is designed to obtain a potential flow with uniform velocity far upstream, far downstream and a prescribed \(\partial W/\partial z(x,0,0)\) gradient along the line \(y=0\) and \(z=0\).
The flat plate surface, over which the boundary layer studied develops, is on the \(y=0\) plane shown in figure 1. In the laterally converging wall case the duct has a wide rectangular cross-section at the inlet, and which contracts symmetrically in the lateral direction with downstream distance, whilst expanding in the positive \(y\) direction. The laterally diverging case is obtained by simply reversing the duct geometry.
Cross-sections in both cases:
| laterally converging walls | laterally diverging walls | |
|---|---|---|
| inlet | 0.8 m wide by 0.25 m height | 0.4 m wide by 0.5 m height |
| outlet | 0.4 m wide by 0.5 m height | 0.8 m wide by 0.25 m height |
Flow Characteristics
The test-section is placed 500 mm downstream from a 3.5 m long contraction with a contraction ratio of 15 so that the entry flow is mainly two-dimensional. The geometry of the duct is designed to generate a strong convergence or divergence of the flow on the flat floor of the test-section without risk of flow separation under the roof. The secondary flow is generated by the lateral streamline curvature and the development of the three-dimensional boundary layers on the floor is mainly pressure-driven.
After being smoothly distorted along the transition, the flow finally relaxes towards two-dimensionality at outlet. The boundary layer is thickened in the case of convergence and thinned in case of divergence.
Flow Parameters
- Air at temperature: \(T = 28\)oC.
- Inlet free-stream velocity: \(U_o = 42\) m/s.
- Barometric pressure: \(p = 967\) hPa.
- Kinematic viscosity: \(\nu = 1.7 \times 10^5\) m2/s.
- Density: \(\rho = 1.11\) kg/m3.
Inflow Conditions
At station \(x = 0\), the flow is largely two-dimensional, with boundary layer features:
- boundary-layer thickness: \(\delta = 16\) mm
- boundary-layer displacement thickness: \(\delta_1 = 2.3\) mm
- boundary-layer momentum thickness: \(\delta_2 = 1.7\) mm
- free stream turbulence level: 0.1%
The following measurements are available for the turbulent boundary layer on the bottom wall:
- Contour maps of mean velocity for \(y\) up to 80 mm (in file 2_p3c01.dat for the 2D case, files 3c_p3c01.dat and 3c_p5x01.dat for the converging case, and files 3d_p3c01.dat and 3d_p5x01.dat for the diverging case).
- Profiles in the symmetry plane \(z = 0\) for \(y\) up to 25 mm of the Reynolds stresses and third order moments (in files 2_hws01.dat and 2_hws02.dat for the 2D case, files 3c_hws01.dat and 3c_hws02.dat for the converging case, and files 3d_hws01.dat and 3d_hws02.dat for the diverging case).
Experimental Details
Measured Quantities:
Wall static pressures (file names containing pst) have been measured through 0.8 mm tappings. The pressure coefficient is defined as \(C_p = (p - p(2500,0,0))/(0.5\rho U(0,80,0)^2)\).
Wall shear stresses (file names containing cf) have been measured using either Preston tubes with diameters of 0.5 mm and 1 mm or a floating-element balance.
Velocities have been measured using either a rotatable crossed-hot-wire or a simple crossed-hot-wire probe (file names containing hw), a three-hole pressure probe (file names containing p3) and a five-hole (file names containing p5) pressure probe.
Measurement Errors:
| \(\delta(\text{probe positions})\) | \(\pm 0.05\) mm |
| \(\delta(\text{angles})\) | \(\pm 0.3^o\) |
| \(\delta(p)\) | \(\pm 1\) Pa |
| \(\delta(C_f)\) | \(\pm 2\%\) |
| \(\delta(\text{mean velocities})\) | \(\pm 2\%\) |
| \(\delta(\text{Reynolds stresses})\) | \(\pm 10\%\) |
Available Measurements
Data available include:
- Wall pressure and skin friction coefficients for the 2D and laterally converging and diverging cases
- Mean velocity profiles across the ducts at a number of streamwise and spanwise locations
- Reynolds stress profiles at a selection of streamwise locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The data are contained in a number of files detailed in the table below. The file info.dat contains some further description of the files and content.
Apart from the geometry files, those with names starting “2_” correspond to the 2D boundary layer case, those starting with “3c_” correspond to the laterally converging walls case, and those starting with “3d_” correspond to the laterally diverging walls case.
| Nozzle Geometry | ||
|---|---|---|
| Profile | Case | File |
| Computed lateral wall streamline on \(y=0\) | 3Dc | bott_c01.dat |
| Computed upper wall streamline | 3Dc | roof_c01.dat |
| Measured lateral wall streamline on \(y=80\) mm | 3Dc | bott_m01.dat |
| Measured lateral wall streamline on \(y=40\) mm | 3Dc | bott_m02.dat |
| Measured lateral wall streamline on \(y=8\) mm | 3Dc | bott_m03.dat |
| Measured lateral wall streamline on \(y=40\) mm | 3Dd | bott_m04.dat |
| Measurements | ||||
|---|---|---|---|---|
| 2D Case | Laterally Converging Case | Laterally Diverging Case | ||
| Wall Pressure Measurements | ||||
| Static wall pressure | 2_pst01.dat | 3c_pst01.dat | 3d_pst01.dat | Traverses across the duct, at a number of streamwise, \(x\), locations |
| Friction Coefficient \(C_f\) ( mostly from Preston tube, \(D=1\) mm) | ||||
| \(C_f\) Spanwise at \(x=0\) mm | 2_cfc01.dat | 3c_cfc01.dat | 3d_cfc01.dat | |
| \(C_f\) Spanwise, \(x=1000\) mm | 2_cfc02.dat | |||
| \(C_f\) Spanwise, \(x=2000\) mm | 2_cfc03.dat | |||
| \(C_f\) Spanwise profiles | 3c_cfc02.dat, 3c_cfc03.dat | 3d_cfc02.dat | Traverses across the duct, at a number of streamwise, \(x\), locations | |
| \(C_f\) Streamwise, \(z=0\) | 2_cfs01.dat | 3c_cfs01.dat | 3d_cfs01.dat | Along duct centreline, from Preston tube |
| \(C_f\) Streamwise, \(z=0\) | 2_cfs02.dat | 3c_cfs02.dat | 3d_cfs02.dat | Along duct centreline, from skin friction balance |
| Boundary Layer Integral Properties | ||||
| Integral Properties, \(z=0\) | 2_p1s02.dat | 3c_p1s02.dat | 3d_p1s02.dat | \(U_e\), \(\delta\), \(\delta^*\), \(\delta_{\theta}\), \(H_{12}\), \(H_{23}\) along duct centreline |
| Integral Properties, \(x=0\) | 2_p3c03.dat | Values at selected \(z\) locations on the inlet plane | ||
| Mean Velocity Profiles | ||||
| Vel. Profiles, \(z=0\) | 2_p1s01.dat | 3c_p1s01.dat | 3d_p1s01.dat | Profiles at selected \(x\) locations on centreline, from Preston tube |
| Vel profiles, \(x=0\) | 2_p3c01.dat | 3c_p3c01.dat | 3d_p3c01.dat | Profiles at selected \(z\) locations, from 3-hole probe |
| Vel profiles, \(x=50\) mm | 3c_p3c02.dat | 3d_p3c02.dat | Profiles at selected \(z\) locations, from 3-hole probe | |
| Vel profiles, \(x=900\) mm | 3c_p3c03.dat | 3d_p3c03.dat | Profiles at selected \(z\) locations, from 3-hole probe | |
| Vel profiles, \(x=1000\) mm | 3c_p3c04.dat | 3d_p3c04.dat | Profiles at selected \(z\) locations, from 3-hole probe | |
| Vel profiles, \(x=1100\) mm | 3c_p3c05.dat | 3d_p3c05.dat | Profiles at selected \(z\) locations, from 3-hole probe | |
| Vel profiles, \(x=2000\) mm | 2_p3c02.dat | Profiles at selected \(z\) locations, from 3-hole probe | ||
| Vel profiles, \(x=2500\) mm | 3c_p3c06.dat | 3d_p3c06.dat | Profiles at selected \(z\) locations, from 3-hole probe | |
| Vel profiles, \(z=-200\) mm | 3c_p3s01.dat, 3c_p3s11.dat | 3d_p3s01.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=-150\) mm | 3c_p3s02.dat | 3d_p3s02.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=-100\) mm | 3c_p3s03.dat | 3d_p3s03.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=-0\) mm | 3c_p3s04.dat | 3d_p3s04.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=100\) mm | 3c_p3s05.dat | 3d_p3s05.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=150\) mm | 3c_p3s06.dat | 3d_p3s06.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(z=200\) mm | 3c_p3s07.dat, 3c_p3s71.dat | 3d_p3s07.dat | Profiles at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(y=0.2\) mm | 3c_p3y03.dat | 3d_p3y03.dat | Profiles across the duct at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(y=10\) mm | 3c_p3y02.dat | Profiles across the duct at selected \(x\) locations, from 3-hole probe | ||
| Vel profiles, \(y=100\) mm | 3c_p3y01.dat | 3d_p3y01.dat | Profiles across the duct at selected \(x\) locations, from 3-hole probe | |
| Vel profiles, \(x=0\) mm | 3c_p5x01.dat | 3d_p5x01.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(x=500\) mm | 3c_p5x02.dat | 3d_p5x02.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(x=1000\) mm | 3c_p5x03.dat | 3d_p5x03.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(x=1500\) mm | 3c_p5x04.dat | 3d_p5x04.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(x=2000\) mm | 3c_p5x05.dat | 3d_p5x05.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(x=2500\) mm | 3c_p5x06.dat | 3d_p5x06.dat | Profiles at selected \(z\) locations, from 5-hole probe | |
| Vel profiles, \(y=100\) mm | 3c_p5y01.dat | 3d_p5y01.dat | Profiles across the duct at selected \(x\) locations, from 5-hole probe | |
| \(U_e(x,z)\), \(z>0\) | 3c_p5e01.dat | 3d_p5e01.dat | Boundary layer edge velocity, from 5-hole probe | |
| \(U_e(x,z)\), \(z<0\) | 3c_p5e02.dat | 3d_p5e02.dat | Boundary layer edge velocity, from 5-hole probe | |
| Hot Wire Measurements of Mean Velocity and Turbulence Statistics (Reynolds, stresses, triple moments, flatness, skewness) | ||||
| Centreline profiles | 2_hws01.dat | 3c_hws01.dat | 3d_hws01.dat | From X-wire on the \((U,V)\) plane |
| Centreline profiles | 2_hws02.dat | 3c_hws02.dat | 3d_hws02.dat | From X-wire on the \((U,W)\) plane |
| Profiles at \(x=1000\) mm | 3c_hwc01.dat | 3d_hwc01.dat | From rotatable X-wire | |
Recommendations for Calculations
Inlet Conditions: The calculation can be started at \(x = 0\) using the experimental values provided as inlet conditions. These values correspond to a 2D turbulent boundary layer. For the region close to the wall (\(0 \le y \le 3\) mm), the values of the turbulent quantities are not measured and the value of \(k\) may need to be approximated. An alternative is to perform a separate flat plate boundary layer calculation and extract profiles from that at an appropriate stage of development.
Symmetry: Due to geometric symmetry with respect to the \(z=0\) plane one can use a computational domain of only one half of the test-section.
Outlet Conditions: The rectangular duct has a constant cross-section beyond the section \(x = 2500\) mm. The outlet section may be moved sufficiently far downstream in order to assume zero streamwise gradients for the flow variables.
Previous Numerical Studies:
The author of the experiments and his coworkers have also performed calculations of the two different flows using a finite-difference boundary layer code (Pompeo et al, 1993). First-order boundary layer equations have been used with the turbulent viscosity equations of Cebeci and Smith (1968). In the case of the diverging walls, good agreement with the experimental results has been found without any particular problem. In the case of the converging walls, the choice of the boundary conditions at the outer edge of the boundary layer has been found to have a considerable influence on the computed results and good agreement has only been obtained after several adjustments of the constants of the model.
Main References
- Pompeo, L.P. (1992). An experimental study of three-dimensional turbulent boundary layers. Diss. ETH, Zurich No. 9780.
- Pompeo, L.P., Bettelini, M.S.G., Thomann, H. (1993). Laterally strained turbulent boundary layers near a plane of symmetry. J. Fluid Mech., Vol. 257, pp. 507-532.
Indexed data:
| case017 (dbcase, semi_confined_flow, confined_flow) | |
|---|---|
| case | 017 |
| title | Laterally Strained Boundary Layers |
| author | Pompeo, Bettelini, Thomann |
| year | 1992 |
| type | EXP |
| flow_tag | 3d, 3dbl, varying_cross_section |