Table of Contents
2D Channel Flow with/without Thermal Field
DNS by Kasagi, Tomita, Kuroda, Ohtsubo
Description
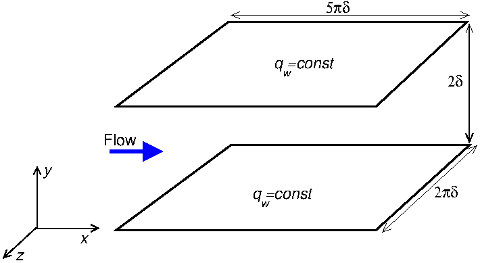
The cases here consist of DNS studies of fully developed plane channel flow, as shown in figure 1. The dynamic field is reported at two Reynolds numbers (\(Re_{\tau}=100\) and \(150\)). For the higher Reynolds number case the fully developed thermal field is also reported, for molecular Prandtl numbers of 0.71 an 0.025. These conditions are summarized in the table below.
| Cases | |||
|---|---|---|---|
| \(Re_{\tau}\) | 100 | 150 | |
| \(Re_{bulk}\) | 2980 | 4560 | |
| \(Pr\) | - | 0.71 | 0.025 |
For the thermal field calculations isoflux conditions were imposed on the two walls, so the local mean temperature increased linearly in the streamwise direction. With any buoyancy effect neglected, temperature was considered as a passive scalar.
Simulation Details
The flow geometry and the co-ordinate system are shown in figure 1. Note that \(y\) denotes the distance from the bottom wall normalised by the channel half width \(\delta\); i.e., \(y = 0\) and \(2\) at the two walls.
The Reynolds number \(Re\), based on the wall friction velocity \(u_{\tau}\) and \(\delta\) was set to be 100 and 150 in the two cases. The resultant bulk Reynolds numbers \(Re_{bulk}\) were approximately 2980 and 4560 respectively.
Referring to the numerical procedure used by Kim et al. (1987), a fourth-order partial differential equation for \(v\), a second-order partial differential equation for the wall-normal component of vorticity \(\omega_y\) and the continuity equation were used to solve the flow field.
A spectral method with Fourier series in the \(x\) and \(z\) directions and a Chebyshev polynomial expansion in the wall-normal direction were used. For the \(Re_{\tau}=150\) case the computational periods were chosen to be \(5\pi\delta\) and \(2\pi\delta\) (2356 and 942 in wall units) in the \(x\) and \(z\) directions, respectively. \(128 \times 128\) Fourier modes and Chebyshev polynomials up to the order 96 in wave number space were used in order to resolve all essential turbulent scales on the computation grid. The collocation grid used to compute the nonlinear terms in physical space had 1.5 times finer resolution in each direction to remove aliasing errors. This resulted in effective grid spacings of: \(\Delta x^+ \approx 18.4\), \(\Delta y^+ = 0.05\) to \(4.9\), and \(\Delta z^+ \approx 7.4\) in the three directions.
For time integration, the second-order Adams-Bashforth and Crank-Nicolson schemes were adopted for the nonlinear and viscous terms, respectively.
Available Data
The available data include:
\(Re_{\tau}=100\) Case:
- Mean velocity and Reynolds stress profiles across the channel
- Skewness and flatness factors
- Turbulent kinetic energy budget
\(Re_{\tau}=150\) Case:
- Mean velocity and Reynolds stress profiles across the channel
- Mean temperature, turbulent heat fluxes and temperature variance profiles
- Skewness and flatness factors
- Budgets of Reynolds stresses, turbulent kinetic energy and its dissipation rate
- Budgets of turbulent heat fluxes, temperature variance and its dissipation rate
- One dimensional energy spectra at selected \(y^+\) locations
- Two-point correlations at selected \(y^+\) locations
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| \(Re_{\tau}=100\) | \(Re_{\tau}=150\) | |
| Dynamic field | ch12_pg_wl2.dat | ch12_pg_wl1.dat |
| Thermal field, \(Pr=0.71\) | ch122_pg_wl1.dat | |
| Thermal field, \(Pr=0.0.25\) | ch122_pg_wl2.dat |
References
- Kasagi, N., Tomita, Y., Kuroda, A. (1991). Direct numerical simulation of the passive scalar field in a two-dimensional turbulent channel flow. Proc. 3rd ASME/JSME Thermal Engineering Joint Conference.
- Kasagi, N., Tomita, Y., Kuroda, A. (1992). Direct numerical simulation of passive scalar field in a turbulent channel flow. ASME J. Heat Transfer, Vol. 114, p. 598.
- Kasagi, N., Ohtsubo, Y., Tomita, Y. (1991). Direct numerical simulation of the low Prandtl number scalar field in a two dimensional turbulent channel flow. Proc. 8th Turbulent Shear Flow Symposium, Munich, Germany.
- Kim, J., Moin, P., Moser, R. (1987). Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech., Vol. 177, pp. 133-166.
Indexed data:
| case045 (dbcase, confined_flow) | |
|---|---|
| case | 045 |
| title | 2D Chanel Flow with/without Thermal Field |
| author | Kasagi, Tomita, Kuroda, Ohtsubo |
| year | 1992 |
| type | DNS |
| flow_tag | scalar, constant_cross_section, channel_flow |