Table of Contents
Separated Turbulent Flow Over a Wavy Wall
DNS by Maaß and Schumann
Description
The impact of a wavy surface on turbulent flow is investigated by direct numerical simulations. By means of finite differences in terrain following coordinates, the method treats the flow in a plane channel with wavy lower and flat top surface. Both surfaces are smooth. The lower surface wave amplitude is 0.05 and the wavelength is 1 in units of the mean channel height. The Reynolds number in terms of mean velocity and mean channel height is 6760. At this Reynolds number an intermittent recirculation occurs. These parameters and flow conditions are, apart from the exact surface shape, similar to those reported by Hudson et. al (1996). (See Case 76 of this database).
Simulation Method
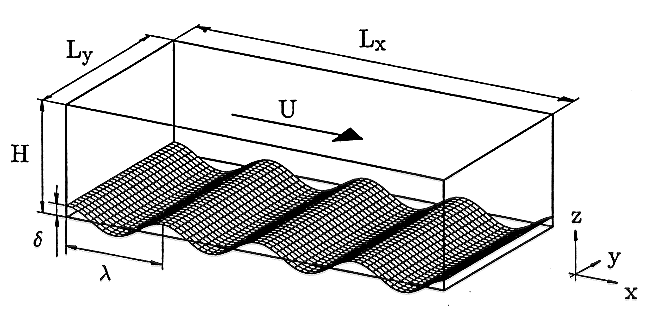
The basic model equations are given by the continuity equation and the momentum balance for an incompressible fluid. These equations are formulated for the Cartesian velocity components as a function of curvilinear coordinates. Here, \(\eta = H(z-h)/(H-h)\) maps the domain between the wavy bottom surface at height \(h(x,y)= \delta \cos(2\pi x/\lambda)\) and the plane top surface at \(z = H\) onto a rectangular transformed domain.
The geometrical parameters are the mean channel height \(H\), the lateral length \(L_z\) and streamwise length \(L_x\), the wave amplitude \(\delta\), and the wavelength \(\lambda\), see figure 1. To get higher resolution at the rigid surfaces an additional hyperbolical transformation was used, so that two adjacent grid spacings \(\Delta \eta\) differed by less than 7%.
The differential equations were approximated by finite differences on a spatial staggered grid. The first discrete grid point for the horizontal velocity components was located \(\Delta \eta/2\) above the wall. The momentum equation was integrated in time using the Adams-Bashforth scheme. The mean velocity \(U\) is defined as the average velocity in the \(x\) direction across a \(y\)-\(z\) plane at a position with vanishing wave amplitude. After each time step \(\Delta t\), the actual mean velocity was tested and a mean pressure gradient in the axial direction calculated such that \(U\) should remain constant. The pressure was determined iteratively. After five iterations the divergence in the first grid level above the bottom surface was reduced to \(1.5\times 10^{-6} U/H\). At other grid levels it was lower by an order of 3 magnitudes.
Periodicity conditions were used at the lateral and streamwise boundaries. At the bottom and top surfaces the no-slip condition was implemented.
The method is described in detail by Krettenauer and Schumann (1992).
Parameters
The main computational parameters of the DNS are:
| mean channel height | \(H = 1\) |
| channel width | \(L_y = 2\) |
| channel length | \(L_x = 4\) |
| wave amplitude | \(\delta = 0.05\) |
| wavelength | \(\lambda = 1\) |
| number of meshes | \(N = 256 \times 128 \times 96\) |
| timestep | \(\Delta t = 0.003\) |
| mean velocity | \(U_b = 1\) |
| density | \(\rho = 1\) |
| Reynolds number | \(Re = U H/\nu = 6760\) |
All values are made dimensionless with channel height \(H\) and mean velocity \(U_b\).
The horizontal mesh size in terms of wall units was \(\Delta x^+=10.9\). The minimal mesh height in terms of wall units was \(\Delta \eta^+ =1.6\). The friction velocities calculated from the total drag are \(u_{\tau}=0.070\) and \(0.104\) at the flat and wavy boundary, respectively.
Available Data
Data available includes profiles at 10 streamwise locations of mean velocities, Reynolds stresses, and mean and rms pressures.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt contains some description of the files.
| Location | File |
|---|---|
| \(x/\lambda=0.101\) | dat01.dat |
| \(x/\lambda=0.195\) | dat02.dat |
| \(x/\lambda=0.304\) | dat03.dat |
| \(x/\lambda=0.398\) | dat04.dat |
| \(x/\lambda=0.492\) | dat05.dat |
| \(x/\lambda=0.601\) | dat06.dat |
| \(x/\lambda=0.695\) | dat07.dat |
| \(x/\lambda=0.804\) | dat08.dat |
| \(x/\lambda=0.898\) | dat09.dat |
| \(x/\lambda=0.992\) | dat10.dat |
References
- Hudson, J.D., Dykhno, L., Hanratty, T.J. (1996). Turbulence production in flow over a wavy wall. Experiments in Fluids, Vol. 20, pp. 257-265.
- Krettenauer, Schumann (1992). Numerical simulation of turbulent convection over wavy terrain. J. Fluid Mech., Vol. 237, pp. 261-299.
- Maaß, C., Schumann, U. (1994). Numerical simulation of turbulent flow over a wavy boundary, in Direct and Large-Eddy Simulation 1 (eds. Voke, Kleiser and Chollet), Kluwer.
- Maaß, C., Schumann, U. (1996). Direct numerical simulation of separated turbulent flow over a wavy boundary, in Flow simulation with high performance computers (ed. Hirschel, E.H.)
Indexed data:
| case077 (dbcase, confined_flow) | |
|---|---|
| case | 077 |
| title | Separated turbulent flow over a wavy wall |
| author | Maaß, Schumann |
| year | 1995 |
| type | DNS |
| flow_tag | 2d, separated, varying_cross_section |