Flow Over a Wavy Wall
Experiment by Hudson, Dykhno and Hanratty
Description
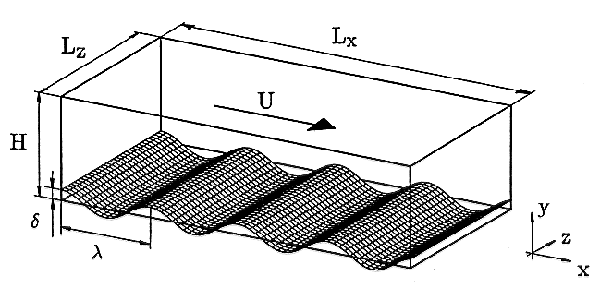
Measurements of the spatial and time variation of two components of the velocity have been made over a sinusoidal solid wavy boundary (see figure 1) with a height to length ratio of \(2\delta/\lambda =0.10\) and with a dimensionless wave number of \(\alpha^+ = (2\pi/\lambda)(\nu/u^*)=0.02\).
The experiment was made in a rectangular water channel. The test section was preceded by a developing section of about 100 channel heights. The lower wall was constructed with removable Plexiglas plates on which the waves were milled. The LDV measurements were made above the 31st of 36 waves to ensure that a fully periodic flow had developed.
The Reynolds number was set to \(Re_H=U_bH/\nu = 6760\), where \(H\) is the channel height \(U_b\) the bulk velocity, so as to be in a region where separation of the mean flow occurs.
For corresponding DNS results see Case 77 of this database, and for a comparison between the two see Maaß & Schumann (1996).
Parameters
The parameters of the experiment are:
| mean channel height | \(H = 50.8\) mm |
| channel width | \(L_z = 610\) mm |
| wave amplitude | \(\delta = 2.54\) mm |
| wavelength | \(\lambda = 50.8\) mm |
| bulk velocity (lower half) | \(U =120\) mm/s |
| Reynolds number | \(Re = U_bH/\nu = 6760\) |
Experimental Details
The measurements were made in a rectangular water channel with a cross section of 5.08 by 61 cm. The test section was preceded by a developing section of approximately 100 channel heights in length to ensure a fully developed flow. The lower wall was constructed with removable Plexiglas plates on which were milled sinusoidal waves of length 5.08 cm and amplitude approximately equal to \(0.05\lambda\). The measurements were made above the 31st of 36 waves to ensure a fully periodic flow field. Details on the channel construction are given by Niederschulte (1988).
The LDV system used in the experiments (Niederschulte et al., 1990) consisted of a 35 mW Spectra Physics He-Ne laser and TSI optics which used polarisation rotation to achieve channel separation. The three beam, two component, system was operated in the forward scatter mode. Flow reversals were detected by the use of a Bragg (acousto-optic) cell with electronic downmixing. Measurements with this system in a channel flow have been used to check the accuracy of direct numerical simulations.
The wave steepness was \(2\delta/\lambda = 0.1\). The Reynolds number, \(Re_h = U_bh/\nu\), was set at 3380 so as to be in a region where separation of the mean flow occurs, according to the map of Zilker & Hanratty (1979). Here \(U_b\) is the bulk-averaged velocity, equal to 12.0 cm/s, and \(h\) is the half-height of the channel. The Reynolds number based on the hydraulic diameter would be 13360. This Reynolds number was chosen for an initial study because a direct numerical simulation could be carried out for the same conditions and because details of the flow very close to the wall could be resolved. All of the measurements of \(U\), \(V\), \(\overline{u^2}\), \(\overline{v^2}\) and \(\overline{uv}\) are tabulated in the thesis by Hudson (1993).
The exact location of the crest of the waves relative to the optical measurement volume was difficult to determine; therefore, the \(x = 0\) reported in the experimental results need not correspond exactly to the crest. The wave profile, determined by the intersection of the laser beams with the surface, was measured, and through fitting this by a cosine curve it was determined that \(x/\lambda=0\) corresponds approximately to a location 1.2 mm downstream of the wave crest. The wave surface profile can correspondingly be taken as
\[ \frac{y-y_o}{h} = 0.1 \cos(2\pi x/\lambda+0.144) \]
where \(y_o\) is the mean location of the wavy channel base.
Available Measurements
Data available includes profiles at 10 streamwise locations of:
- Mean velocities \(U\) and \(V\)
- Rms velocities \(u'\), \(v'\), and Reynolds shear stress \(\overline{uv}\)
- Skewness and Flatness factors
- Pressure, calculated from the velocity data
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt contains some description of the files.
| Location | File |
|---|---|
| \(x/\lambda=0.0\) | xlam00.dat |
| \(x/\lambda=0.1\) | xlam01.dat |
| \(x/\lambda=0.2\) | xlam02.dat |
| \(x/\lambda=0.3\) | xlam03.dat |
| \(x/\lambda=0.4\) | xlam04.dat |
| \(x/\lambda=0.5\) | xlam05.dat |
| \(x/\lambda=0.6\) | xlam06.dat |
| \(x/\lambda=0.7\) | xlam07.dat |
| \(x/\lambda=0.8\) | xlam08.dat |
| \(x/\lambda=0.9\) | xlam09.dat |
| Calculated pressure data | pressure.dat |
References
- Hudson, J.D., Dykhno, L., Hanratty, T.J. (1996). Turbulence production in flow over a wavy wall. Experiments in Fluids, Vol. 20, pp. 257–265.
- Hudson, J.D. (1993). The effect of a wavy boundary on turbulent flow. PhD thesis, Dept. of Chemical Engineering, University of Illinois, Urbana.
- Maaß, C., Schumann, U. (1996). Direct numerical simulation of separated turbulent flow over a wavy boundary, in Flow simulation with high performance computers (ed. Hirschel, E. H.); Notes on numerical fluid mechanics, 52; pp 227–241.
- Niederschulte, M.A. (1988). Turbulent flow through a rectangular channel. PhD Thesis, Univ. of Illinois, Urbana.
- Niederschulte, M.A., Adrian, R.J., Hanratty, T.J. (1990). Measurements of turbulent flow in a channel at low Reynolds numbers. Exp. Fluids, Vol. 9, pp. 222-230.
- Zilker, D.P., Hanratty, T.J. (1979). Influence of the amplitude of a solid wavy wall on a turbulent flow. Part 2. Separated flows. J. Fluid Mech., Vol. 90, pp. 257-271.
Indexed data:
| case076 (dbcase, confined_flow) | |
|---|---|
| case | 076 |
| title | Flow over a wavy wall |
| author | Hudson, Dykhno, Hanratty |
| year | 1995 |
| type | EXP |
| flow_tag | 2d, separated, varying_cross_section |