Pulsed Channel Flow
Experiments by Tardu, Binder, Feng, Vezin, Blackwelder
Description
Tardu et al (1994) report measurements in turbulent channel flow with forced oscillations covering a range of frequencies (\(\omega^+ = 0.03-0.0005\)) and amplitudes (10-70 % of centreline velocity). Phase averages of the velocity (\(<u>\)) across the flow, and of the wall shear stress (\(<\tau>\)), as well as the turbulent fluctuations (\(<u'u'>\)) and (\(<\tau'\tau'>\)) are obtained with LDA and hot-film techniques.
Experimental Details
The main elements of the flow loop apparatus are shown in figure 1 and are: a constant-head tank with a large free surface in order to minimize variations in the total head when flow is pulsed, the pulsator, a control valve, a settling chamber with screens and a honeycomb, a converging section with a 10:1 contraction, the test channel, a large free-surface tank (1 x 2 x 4.5 m3) and the pump. The last metre of the channel is immersed in this tank. A divergence up to 30o can be imposed on this section to set up a time-mean pressure gradient. The return flow to the pump is via a free-surface flow in order to limit the elements of the loop subjected to large unsteady pressure forces.
The dimensions of the test channel are : height = 100 mm, length = 2600 mm, span = 1000 mm. The boundary layer at the channel entrance is tripped by tridimensional 5 mm high crenel-type roughnesses.
Oscillations in the flow rate were produced by the device shown in figure 1. The inflow pipe to the pulsator terminates in a cylinder having 24 longitudinal 5 x 200 mm slots machined in its surface as shown. The end of the cylinder was capped so the water had to exit through the slots. A moveable sleeve was tightly fitted around the cylinder so the sleeve covered some, all or none of the length of the slots. This apparatus was housed inside a larger cylinder, which collected the water exiting through the slots and allowed it to continue into the settling chamber. The oscillation frequency of the sleeve was controlled by a variable-speed motor through an eccentric bearing. The eccentricity was adjustable to control the amplitude of the oscillation, and the mean flow was controlled by adjusting the length of the connecting arm between the eccentric bearing and the sleeve. These three variables were easily changed in a continuous manner to adjust the flow conditions. The amplitude could be varied from 0 to 80% of the mean flow and the period from 2.5 s to infinity, although the largest period studied was 132 s.
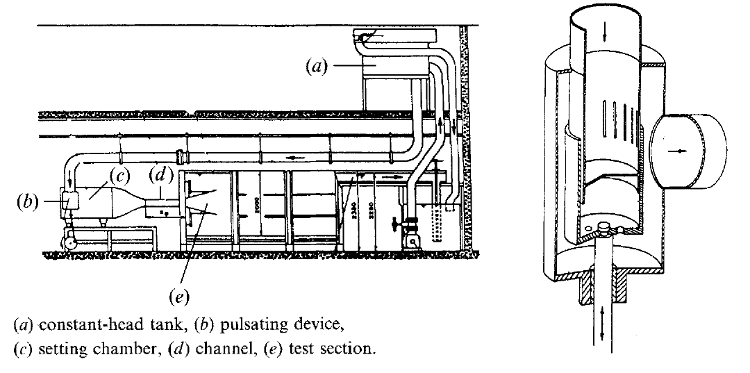 Fig. 1: Schematic of the experimental flow rig
Fig. 1: Schematic of the experimental flow rig
The streamwise velocity was measured by a one-component 25 mW laser Doppler anemometer. The dimensions of the measuring volume were 0.3 and 1.5 mm. These dimensions could be reduced by a factor of 5 by use of a 5X-beam expander. Measurements as close as 0.25 mm (approximately \(2.5l_v\) for \(\overline{U}_c = 17.5\) cm/s) were then possible, but not without difficulty because the signal quality very close to the wall was poor and the sampling rate quite small (a few samples/s).
The wall shear stress \(\tau\) was measured with Dantec 55R46 or TSI 1268 W flush- mounted hot-film probes (sensing surfaces 0.2 x 0.75 mm and 0.127 x 1 mm respectively). They were operated at overheat ratios between 3 and 8% with Disa 55M01 or Dantec 56C01 constant-temperature anemometers.
Flow Parameters
The complexity of these unsteady wall flows is reflected in the difficulty in establishing which similarity parameters are physically the most relevant, and the fact that different studies have used different characterisation parameters.
Parameters frequently used include the viscous Stokes layer thickness, \(l_s=\sqrt(2\nu/\omega)\), where \(\omega=2\pi f\) is the frequency of the imposed oscillation. This can be expressed non-dimensionally as \(l_s^+=l_s \overline{u}_{\tau}/\nu\) where \(\overline{u}_{\tau}\) is the time-averaged wall friction velocity. The forcing frequency \(\omega\) is also sometimes expressed in non-dimensional form as \(\omega^+=\omega \nu/(\overline{u}_{\tau})^2 = 2/(l_s^+)^2\).
The data has been processed via the usual decomposition into time-mean, periodic and random turbulent parts, so the quantity \(q\) is decomposed as \[ q(y,t) = \overline{q}(y) + \tilde{q}(y, t/T) + q'(y,t) \]
Angled brackets are used to denote the ensemble or phase average: \[ <q(y,t/T)> = \overline{q}(Y) + \tilde{q}(y,t/T) \]
The phase-averaged statistic \(<q'q'>\) is a function of t/T and it is often convenient to write it as \(<q'q'>(t/T) = \overline{q'q'} + \widetilde{q'q'}(t/T)\), where \(\widetilde{q'q'}\) is the ‘modulation' of the variance about the time-mean value \(\overline{q'q'}\). Neither \(\tilde{q}\) nor \(\widetilde{q'q'}\) are necessarily pure sine functions, and are often conveniently described by the amplitudes and phases of the successive terms of a Fourier series. In many cases the fundamental mode is dominant, and an adequate description of the modulation is then given by the amplitude and phase of the fundamental mode, designated by \(A_{\tilde{q}}\) and \(\Phi_{\tilde{q}}\). The relative modulation, i.e. the amplitude of the modulation with respect to the time-mean value of the same quantity, is designated by a lower-case letter \(a_{\tilde{()}}\), for example \(a_\tilde{q} = A_{\tilde{q}}/\overline{q}\) or \(a_{\widetilde{q'q'}} = A_{\widetilde{q'q'}}/\overline{q'q'}\).
The table below details the range of parameters studied by Tardu et al (1994).
| \(\overline{U}_c\) (m/s) | \(f^+\) | \(l_s^+\) | \(a_{\widetilde{U}_c}\) |
| 17.63 | \(9.9345\times 10^{-4}\) | 17.9 | 0.31 |
| 9.54 | \(1.9069\times 10^{-3}\) | 12.9 | 0.08 |
| 15.77 | \(1.5043\times 10^{-2}\) | 4.6 | 0.40 |
| 13.38 | \(3.7849\times 10^{-2}\) | 2.9 | 0.67 |
Available Measurements
Results are presented in graphical form in the references below, but unfortunately have not been provided as electronic data.
References
- Vezin, P., Tardu, S., Binder, G. (1993). Space-time correlations in an unsteady channel flow. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
- Feng, M.Q., Tardu, S., Binder, G. (1993). The fine structure of the Reynolds shear stress in unsteady turbulent channel flow. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
- Tardu, F.S., Binder, G. (1993). Wall shear stress modulation in unsteady turbulent channel flow with high imposed frequencies. Phys. of Fluids A, Vol. 8, pp. 2028-2037.
- Tardu, F.S., Binder, G., Blackwelder, R.F. (1994). Turbulent channel flow with large-amplitude velocity oscillations. J. Fluid Mech., Vol 267, pp. 109-151.
Indexed data:
| case037 (dbcase, confined_flow) | |
|---|---|
| case | 037 |
| title | Pulsed Channel Flow |
| author | Tardu, Binder, Feng, Vezin, Blackwelder |
| year | 1993 |
| type | EXP |
| flow_tag | unsteady, constant_cross_section, channel_flow |