3D Flow in Wedge-Plate Junction
Experiments by Anderson and Eaton
Description
Three dimensional thermal boundary layer ahead and on the side of an upstream-facing wedge. The flow is a 3D flow with temperature variation.
Geometry
The wind-tunnel consists of two parallel planes separated by 11.9 cm with a development section for the preliminary two-dimensional boundary layer and a test-section including the wedge and a heating surface. The geometry is shown in figure 1.
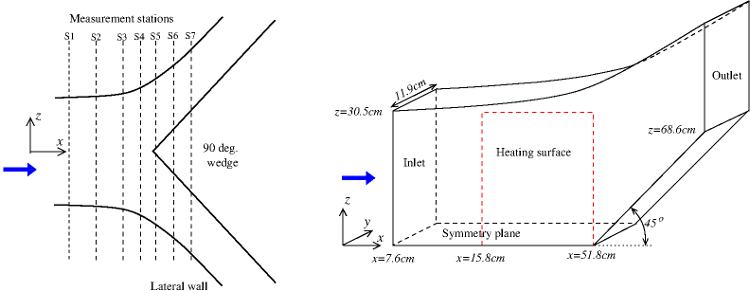 Fig. 1: Wedge geometry. Plan view (left) and 3D view of half the geometry (right)
Fig. 1: Wedge geometry. Plan view (left) and 3D view of half the geometry (right)
The origin of coordinates is the centreline of the test wall at the beginning of the test section and the suggested computational domain covers at least from \(x = 7.6\) cm to \(x = 121.9\) cm. The vertex of the wedge is on the tunnel centreline and its axis is normal to the test wall. The wedge vertex is located at \(x = 51.8\) cm and \(z = 0\) cm. The wedge has a total angle of 90o and is positioned symmetrically so that the freestream is turned by 45o. The wedge extends up to \(x = 121.9\) cm and \(z = \pm 68.6\) cm.
The lateral walls are set so that their position satisfies the fourth-order polynomial: \(z = a + bx + cx^2 + dx^3 + ex^4\) where \(z\) and \(x\) are in cm and \(a = 30.004\) cm, \(b = 0.018957\), \(c = -0.0036287\) cm-1, \(d = 0.00020397\) cm-2 and \(e = -0.00000119\) cm-3.
The primary measurements were all made using probes inserted through seven spanwise slots in the opposite wall of the test section. These slots are referred to as S1-S7 in figure 1, and their axial positions are shown in the following table.
| Slot Position | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| \(x\) (cm) | 7.6 | 22.9 | 38.1 | 45.7 | 53.3 | 61.0 | 68.6 |
The thermal 3D boundary layer is provided by a 36 cm long by 61 cm wide heating surface set up in the test-section immediately in front of the wedge.
Flow characteristics
The three-dimensionality of the flow is due to the transverse pressure gradient created by the wedge facing into the flow and the lateral curved walls. On the centreline, the flow is characterized by a strong adverse pressure gradient when approaching the stagnation point upstream of the wedge. Off centreline, the streamwise pressure gradient is adverse through to station S4, and then becomes favourable as the flow accelerates towards the exit. A strong spanwise pressure gradient develops downstream from the first measurement station and continues throughout the length of the test-section. This causes a monotonic turning of the freestream and a secondary flow within the boundary layer.
The boundary layer for which the measurements have been made develops on the bottom of the test-section designated as the “test wall”.
Flow parameters
- Air with:
- Kinematic viscosity \(\nu = 1.5\times 10^{-5}\) m2/s.
- Density \(\rho = 1.2\) kg/m3.
- Pressure 770 mmHg.
- Nominal free-stream velocity: \(U_{ref}=16.391\) m/s.
- Typical heat-flux: 630 W/m2.
Inflow conditions
The first measurement slot is located at \(x = 7.6\) cm (S1), and the data here could be used to provide inlet conditions, although the boundary layer is reported to be mildly three-dimensional by this location. For those wanting to start calculations further upstream, the boundary layer at the test section entrance is reported to be approximately 3.12 cm thick, with momentum thickness Reynolds number of 3570 and a shape factor of 1.35. The free-stream turbulence intensity is reported to be 0.2%.
Measurements for the boundary layer on the opposite wall are only available at \(x = 2.0\) cm. At this location, it is 2.64 cm thick with a momentum thickness Reynolds number of 2654 and a skin friction coefficient of 0.00388.
The tunnel geometry prevents easy access to the near-wall region of the boundary layer on the side wall so that initial boundary layer measurements on this wall are difficult to perform. Nevertheless, outer layer measurements indicates a boundary layer thickness of approximately 5 cm.
Measurement Techniques
- Mean velocity measurements using a standard three hole pressure probe.
- Turbulent quantity measurements using a rotatable X-array hot-wire probe.
- Static pressure measurements using a standard static pressure probe.
The pressure coefficient is defined as \(C_p = (P-P_o)/P_{dyno}\) where \(P_o\) is the static pressure at the point (\(x=7.6\) cm, \(y=z=0\)) and \(P_{dyno}\) is the dynamic pressure at the same point.
- Temperature measurements using a butt-welded thermocouple probe.
Measurement errors
- \(\delta\)(mean velocities) 3% of local \(U\)
- \(\delta\)(Reynolds normal stresses) 5% of \(\overline{uv}\)
- \(\delta\)(Reynolds shear stresses) 10% of \(\overline{uv}\)
- \(\delta\)(\(\overline{vw}\) near the wall) 15% of \(\overline{uv}\)
Available Measurements
Data available include:
- Wall \(C_p\) values across the duct at the seven streamwise measurement locations
- Cross-stream profiles of \(U\) and \(W\) velocities at several \(y\) locations on the measurement lines
- Wall-normal profiles of \(U\) and \(W\) on the duct centreline
- Profiles of the Reynolds stresses on the centreline at the first measurement station
- Wall-normal profiles of \(U\), \(W\) and temperature at locations following a streamline along the duct
Sample plots of some of the datasets are available.
The data can be downloaded as compressed archive files from the links below, or as individual files from the tables.
The file readme.txt contains some description and details of the data.
| Wall Pressure Coefficients | ||
|---|---|---|
| Station | \(x\) (cm) | File |
| S1 | 7.6 | ncp-x1.dat |
| S2 | 22.9 | ncp-x2.dat |
| S3 | 38.1 | ncp-x3.dat |
| S4 | 45.7 | ncp-x4.dat |
| S5 | 53.3 | ncp-x5.dat |
| S6 | 61.0 | ncp-x6.dat |
| S7 | 68.6 | ncp-x7.dat |
| Mean \(U\) and \(W\) Velocity Profiles across the Duct at Several Wall Distances | ||||||
|---|---|---|---|---|---|---|
| Station | \(x\) (cm) | \(y=0.19\) cm | \(y=0.36\) cm | \(y=0.7\) cm | \(y=1.65\) cm | \(y=5.93\) cm |
| S1 | 7.6 | x1y1-0214d6.dat | x1y2-0214d7.dat | x1y3-0214d8.dat | x1y4-0214d9.dat | x1y5-0214d0.dat |
| S2 | 22.9 | x2y1-0214d1.dat | x2y2-0214d2.dat | x2y3-0214d3.dat | x2y4-0214d4.dat | x2y5-0214d5.dat |
| S3 | 38.1 | x3y1-0215d1.dat | x3y2-0215d2.dat | x3y3-0215d3.dat | x3y4-0215d6.dat | x3y5-0215d5.dat |
| S4 | 45.7 | x4y1-0216d2.dat | x4y2-0216d3.dat | x4y3-0216d4.dat | x4y4-0215d8.dat | x4y5-0215d7.dat |
| S5 | 53.3 | x5y1-0216d6.dat | x5y2-0216d7.dat | x5y3-0216d8.dat | x5y4-0216d9.dat | x5y5-0216d0.dat |
| S6 | 61.0 | x6y1-0216e1.dat | x6y2-0216e2.dat | x6y3-0216e3.dat | x6y4-0216e4.dat | x6y5-0216e5.dat |
| S7 | 68.6 | x7y1-0218d1.dat | x7y2-0218d2.dat | x7y3-0218d3.dat | x7y4-0218d4.dat | x7y5-0218d5.dat |
| Mean \(U\) and \(W\) Velocity and Reynolds Stress Profiles Normal to the Wall on the Duct Centreline | ||||
|---|---|---|---|---|
| Station | \(x\) (cm) | Mean Velocities | Normalized Reynolds Stresses | Dimensional Reynolds Stresses |
| S1 | 7.6 | x1z1-0305d1.dat | 11tcna.dat | 11tcua.dat |
| S2 | 22.9 | x2z1-0404d3.dat | ||
| S3 | 38.1 | x3z1-0823d1.dat | ||
| S4 | 45.7 | x4z1-0423d7.dat | ||
| Mean \(U\), \(W\) and Temperature Profiles Following a Streamline | ||||
|---|---|---|---|---|
| Station | \(x\) (cm) | \(z\) (cm) | Mean Velocities | Mean Temperature |
| S1 | 7.6 | 15 | x1z2-0305d8.dat | 2tx0z0.dat |
| S2 | 22.9 | 15.4 | x2z3-0822db.dat | 2tx1z1.dat |
| S3 | 38.1 | 16.7 | x3z4-1003d1.dat | 2tx2z2.dat |
| S4 | 45.7 | 18.4 | x4z5-1010h2.dat | 2tx3z3.dat |
| S5 | 53.3 | 20.9 | x5z6-1011e1.dat | |
Related Publications
- Anderson, S.D., Eaton, J.K. (1987). Experimental study of a pressure-driven, three-dimensional, turbulent boundary layer. AIAA J., Vol. 25, p. 1086.
- Anderson, S.D., Eaton, J.K. (1989). Reynolds stress development in pressure-driven three-dimensional turbulent boundary layersi. J. Fluid Mech., Vol. 202, pp. 263-294.
- Abrahamson, S.D., Eaton, J.K. (1991). Heat transfer through a pressure-driven three-dimensional boundary layer. J. Heat Transf., Vol. 113, pp. 355-362.
Indexed data:
| case002 (dbcase, semi_confined_flow) | |
|---|---|
| case | 002 |
| title | 3D Flow in Wedge-Plate Junction |
| author | Anderson, Eaton |
| year | 1985 |
| type | EXP |
| flow_tag | 3d, 3dbl, surface_mounted_body |