Circular to Rectangular Transition Duct
Experiments by Davis and Gessner
Description
Turbulent flow in a circular to rectangular transition duct. The flow remains wholly attached along the transition. A 3D flow with constant temperature.
Geometry of the Computational Domain
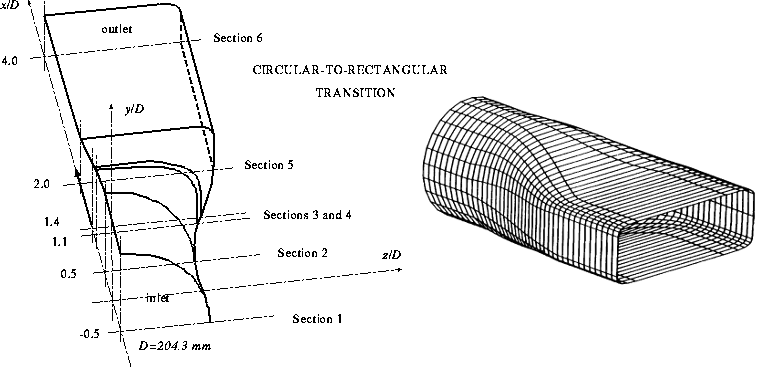
The inlet duct is of length \(0.5D\) and has a circular cross-section of diameter \(D = 2R = 204.3\) mm. The outlet duct is of length \(2D\) with a rectangular cross-section of aspect ratio 3:1. In the transition region, the wall coordinates are given by the superellipse:
\[ \left(y/a \right)^{\eta} + \left( z/b\right)^{\eta} = 1 \]
\(a\), \(b\) and \(\eta\) are functions of the axial distance along the duct, \(x\). The values for \(a\), \(b\) and \(\eta\) are given in the file geom.dat.
The geometry, coordinates, and measurement locations are shown in figure 1.
Flow Characteristics
A secondary flow vortex pair develops in the transition duct which distorts the primary mean velocity and Reynolds stress fields. Analysis of their results by the experimenters shows that in this region conventional wall functions, while applicable, must be used with caution. In the downstream straight duct, the longitudinal vorticity diffuses very rapidly.
Flow Parameters
- Air at atmospheric pressure and temperature \(T = 298.3\) K
- At the inlet:
- axial bulk velocity \(U_b=29.95\) m/s
- kinematic viscosity \(\nu =1.57 \times 10^{-5}\) m2s
- Reynolds number \(Re=U_b D/\nu =3.9 \times 10^5\).
Inflow Conditions
Partially developed turbulent pipe flow at station 1 (\(x/D=-0.5\)).
- Boundary layer features:
- boundary-layer thickness \(\delta/R=0.2855\)
- axisymmetric displacement thickness \(\delta_1/R=0.0383\)
- axisymmetric momentum thickness \(\delta_2/R=0.0281\)
- axisymmetric energy thickness \(\delta_3/R=0.0497\)
- free stream turbulence level of 0.3%
- Friction velocity \(U^*/U_b=0.04063\)
Measured profiles are available for:
- Axial velocity \(U/U_b\)
- Second moments \(\overline{u^2}/U_b^2\), \(\overline{v^2}/U_b^2\), \(\overline{w^2}/U_b^2\), \(\overline{uv}/U_b^2\), \(k/U_b^2\)
Measurement Techniques
Measured quantities:
Wall static pressures have been measured through 0.508 mm tappings. Wall shear stresses have been measured using Preston tubes with different diameters ranging from 1.067 mm to 3.073 mm. Velocities have been measured close to the wall using a single-hot-wire probe rotation technique.
Measurement Errors:
- \(\delta(\text{probe positions}) \pm 0.025\) m.
- \(\delta(\text{angles}) \pm 0.5^o\).
| Variable | Error | Variable | Error |
|---|---|---|---|
| \(\delta(C_p)\) | \( \pm 0.002\) | \(\delta(C_f)\) | \( \pm 0.0005\) |
| \(\delta(U/U_b)\) | \(\pm 0.01\) | \(\delta(V/U_b)\) | \(\pm 0.002\) |
| \(\delta(\overline{u^2}/U_b^2)\) | \(\pm 0.0001\) | \(\delta(\overline{uv}/U_b^2)\) | \(\pm 0.00015\) |
| \(\delta(\overline{v^2}/U_b^2)\) | \(\pm 0.0002\) | \(\delta(\overline{uw}/U_b^2)\) | \(\pm 0.00015\) |
| \(\delta(\overline{w^2}/U_b^2)\) | \(\pm 0.0002\) | \(\delta(\overline{vw}/U_b^2)\) | \(\pm 0.0001\) |
Available Measurements
Measurements were taken at 6 streamwise locations, at \(x/D\) positions given in the table below.
| Station | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \(x/D\) | -0.5 | 0.5 | 1.1 | 1.4 | 2.0 | 4.0 |
Data available for downloading includes:
- Profiles along semi-major and semi-minor axes of:
- Mean velocity \(U\) and pressure at \(x/D=-0.5\), \(1.1\), \(1.4\), \(2.0\), \(4.0\)
- Second moments at \(x/D=-0.5\), \(2.0\), \(4.0\)
- Profiles of circumferential pressure coefficient \(C_p\) at \(x/D=1.1\), \(1.4\), \(2.0\), \(4.0\)
- Profiles of circumferential skin friction coefficient \(C_f\) at \(x/D=2.0\), \(4.0\)
- 2-D maps of
- Mean velocities \(U\), \(V\), \(W\) and pressure at \(x/D=1.1\), \(1.4\), \(2.0\), \(4.0\)
- Second moments at \(x/D=2.0\), \(4.0\)
Sample plots of selected quantities are available.
The data can be downloaded as compressed archive files from the links below, or as individual files by selecting those required from the tables.
Profile Data
| Profile Data at Station 1, \(x/D=-0.5\) | ||||
|---|---|---|---|---|
| Radial Traverse | ||||
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| \(U\) | trd_pr_x1_mu_y1.dat | trd_pr_x1_mu_y2.dat | trd_pr_x1_mu_y3.dat | trd_pr_x1_mu_y4.dat |
| Total Pressure | trd_pr_x1_pt_y1.dat | trd_pr_x1_pt_y2.dat | trd_pr_x1_pt_y3.dat | trd_pr_x1_pt_y4.dat |
| \(\overline{u^2}\) | trd_pr_x1_uu_y3.dat | |||
| \(\overline{v^2}\) | trd_pr_x1_vv_y3.dat | |||
| \(\overline{w^2}\) | trd_pr_x1_ww_y3.dat | |||
| \(k\) | trd_pr_x1_ke_y3.dat | |||
| \(\overline{uv}\) | trd_pr_x1_uv_y3.dat | |||
| Profile Data at Station 3, \(x/D=1.1\) | ||
|---|---|---|
| \(y_2\) (Semi-major axis) | \(y_3\) (Semi-minor axis) | |
| \(U\) | trd_pr_x3_mu_y2.dat | trd_pr_x3_mu_y3.dat |
| Total Pressure | trd_pr_x3_pt_y2.dat | trd_pr_x3_pt_y3.dat |
| \(C_p\) around circumference: | trd_pr_x3_cp.dat | |
| Profile Data at Station 4, \(x/D=1.4\) | ||
|---|---|---|
| \(y_2\) (Semi-major axis) | \(y_3\) (Semi-minor axis) | |
| \(U\) | trd_pr_x4_mu_y2.dat | trd_pr_x4_mu_y3.dat |
| Total Pressure | trd_pr_x4_pt_y2.dat | trd_pr_x4_pt_y3.dat |
| \(C_p\) around circumference: | trd_pr_x4_cp.dat | |
| Profile Data at Station 5, \(x/D=2.0\) | ||
|---|---|---|
| \(y_2\) (Semi-major axis) | \(y_3\) (Semi-minor axis) | |
| \(U\) | trd_pr_x5_mu_y2.dat | trd_pr_x5_mu_y3.dat |
| Total Pressure | trd_pr_x5_pt_y2.dat | trd_pr_x5_pt_y3.dat |
| \(\overline{u^2}\) | trd_pr_x5_uu_y2.dat | trd_pr_x5_uu_y3.dat |
| \(\overline{v^2}\) | trd_pr_x5_vv_y2.dat | trd_pr_x5_vv_y3.dat |
| \(\overline{w^2}\) | trd_pr_x5_ww_y2.dat | trd_pr_x5_ww_y3.dat |
| \(k\) | trd_pr_x5_ke_y2.dat | trd_pr_x5_ke_y3.dat |
| \(\overline{uv}\) | trd_pr_x5_uv_y2.dat | |
| \(\overline{uw}\) | trd_pr_x5_uw_y3.dat | |
| \(C_p\) around circumference: | trd_pr_x5_cp.dat | |
| \(Cf\) around circumference: | trd_pr_x5_cf.dat | |
| Profile Data at Station 6, \(x/D=4.0\) | ||
|---|---|---|
| \(y_2\) (Semi-major axis) | \(y_3\) (Semi-minor axis) | |
| \(U\) | trd_pr_x6_mu_y2.dat | trd_pr_x6_mu_y3.dat |
| Total Pressure | trd_pr_x6_pt_y2.dat | trd_pr_x6_pt_y3.dat |
| \(\overline{u^2}\) | trd_pr_x6_uu_y2.dat | trd_pr_x6_uu_y3.dat |
| \(\overline{v^2}\) | trd_pr_x6_vv_y2.dat | trd_pr_x6_vv_y3.dat |
| \(\overline{w^2}\) | trd_pr_x6_ww_y2.dat | trd_pr_x6_ww_y3.dat |
| \(k\) | trd_pr_x6_ke_y2.dat | trd_pr_x6_ke_y3.dat |
| \(\overline{uv}\) | trd_pr_x6_uv_y2.dat | |
| \(\overline{uw}\) | trd_pr_x6_uw_y3.dat | |
| \(C_p\) around circumference: | trd_pr_x6_cp.dat | |
| \(C_f\) around circumference: | trd_pr_x6_cf.dat | |
| \(C_p\) Along Duct Centerline |
|---|
| trd_pr_cl_cp.dat |
2-D Map Data
| Station 3, \(x/D=1.1\) | Station 4, \(x/D=1.4\) | Station 5, \(x/D=2.0\) | Station 6, \(x/D=4.0\) | |
|---|---|---|---|---|
| \(U\) | trd_co_x3_mu.dat | trd_co_x4_mu.dat | trd_co_x5_mu.dat | trd_co_x6_mu.dat |
| \(V\) | trd_co_x3_mv.dat | trd_co_x4_mv.dat | trd_co_x5_mv.dat | trd_co_x6_mv.dat |
| \(W\) | trd_co_x3_mw.dat | trd_co_x4_mw.dat | trd_co_x5_mw.dat | trd_co_x6_mw.dat |
| Total Pressure | trd_co_x3_pt.dat | trd_co_x4_pt.dat | trd_co_x5_pt.dat | trd_co_x6_pt.dat |
| Static Pressure | trd_co_x5_ps.dat | |||
| \(\overline{u^2}\) | trd_co_x5_uu.dat | trd_co_x6_uu.dat | ||
| \(\overline{v^2}\) | trd_co_x5_vv.dat | trd_co_x6_vv.dat | ||
| \(\overline{w^2}\) | trd_co_x5_ww.dat | trd_co_x6_ww.dat | ||
| \(k\) | trd_co_x5_ke.dat | trd_co_x6_ke.dat | ||
| \(\overline{uv}\) | trd_co_x5_uv.dat | trd_co_x6_uv.dat | ||
| \(\overline{uw}\) | trd_co_x5_uw.dat | trd_co_x6_uw.dat | ||
| \(\overline{vw}\) | trd_co_x5_vw.dat | trd_co_x6_vw.dat |
Previous Solutions
The results of both the calculations of Sotiropoulos and Patel (1993), using a two-layer \(k\)-\(\varepsilon\) model, and Demuen, using a full Reynolds stress closure with wall functions, predict a weaker secondary motion than the measured one.
On the other hand, the results of both the calculations of Lien and Leschziner (1993), using a low-Reynolds \(k\)-\(\varepsilon\) model, and Sotiropoulos and Patel (1993), using the near-wall full-Reynolds stress closure of Launder and Shima, give a good representation of the flow inside the transition and a little bit too rapid decay of the Reynolds stress downstream.
Related Publications
Description of Experiments
- Davis, D.O. (1992). Experimental investigation of turbulent flow through a circular-to-rectangular transition duct. NASA Technical Memorandum 105210.
- Davis, D.O., Gessner, F.B. (1992). Experimental investigation of turbulent flow through a circular-to-rectangular transition duct. AIAA J., Vol. 30, p. 367.
- Davis, D.O., Gessner, F.B. (1990). Experimental investigation of turbulent flow through a circular-to-rectangular transition duct. AIAA Paper 90-1505.
Previous Numerical Calculations
- Lien, F.S., Leschziner, M.A. (1993). Computational modelling of 3D turbulent flow in S. diffuser and transition ducts. 2nd Int. Symp. on Engineering Turbulence Modelling and Measurements, May 31 - June 2.
- Sotiropoulos, F., Patel, V.C. (1993). Numerical calculation of turbulent flow through a circular-to-rectangular transition duct using advanced turbulent closures. AIAA paper 93-3030.
- Lien, F.S., Leschziner, M.A. (1993). Modelling the flow in a transition duct with a non orthogonal FV procedure and low-Re turbulence-transport models. UMIST report TFD/93/10.
- Sotiropoulos, F., Patel, V.C. (1994). Prediction of turbulent flow through a transition duct using a second-moment closure. AIAA J., Vol. 32, p. 2194.
Indexed data:
| case007 (dbcase, confined, flow) | |
|---|---|
| case | 007 |
| title | Circular to Rectangular Transition Duct |
| author | Davis, Gessner |
| year | 1990 |
| type | EXP |
| flow_tag | 3d, separated, varying_cross_section |