Couette Flow with Fixed Wavy Wall
Experiments by Nakabayashi, Kitoh and Iwata
Description
Experimental work has been performed to investigate turbulent Couette-type flow with repeated longditudinal pressure gradients that are realized in a channel consisting of a wavy fixed wall on one side and a moving wall on the other.
This type of flow simulates the flow in high speed journal bearings operating in turbulent conditions. 2D flow with constant temperature.
Geometry
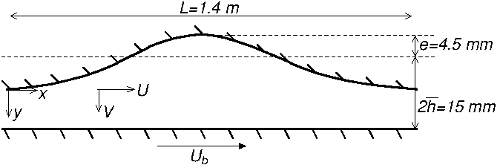
The geometry of the channel, and coordinate system used, are shown in figure 1. The channel has its lower wall moving and its upper wall wavy and fixed.
The test section is \(L = 1.4\) m long (one wavelength) with a mean height (distance between the two walls) of \(2h = 15\) mm.
The fixed wavy wall is approximated by \(y = 2h - e\,cos(2\pi x/L)\) with \(e = 4.5\) mm, although an accurate set of spline fitting functions is provided in the file geom1c.dat.
The measurements have been carried out in the middle part of the channel (total length of 3.5 times the wavelength) in order to minimize upstream and downstream effects. The pressure has been found to be the same at the inlet and outlet of the considered one wavelength-long portion. Moreover the longitudinal pressure gradient is also found to be periodic.
The mean velocity distributions and turbulent intensities are measured at various streamwise positions of \(x/l\) for a Reynolds number \(Re=2hU_b/\nu=8000\). Non-dimensional pressure gradient parameters \(u^{-1} = (\nu dp/dx)/(\rho (U^*)^3)\) can be seen in the table below.
| \(x/l\) | 0 | 0.125 | 0.250 | 0.375 | 0.500 | 0.625 | 0.750 | 0.875 |
|---|---|---|---|---|---|---|---|---|
| \(u^{-1}\) | -0.009 | 0.017 | 0.025 | 0.026 | 0.018 | -0.016 | -0.015 | -0.023 |
Inflow Conditions
Profiles from the fixed wall to moving wall at \(x=0\) are in provided in the file couette.dat of:
- First order moments: \(U\), \(V\)
- Second order moments: \(\overline{u^2}\), \(\overline{v^2}\)
Experimental Details
All velocity measurements were made using hot-wire anemometer.
Measurement Errors
Measurement errors are not published in any English language paper.
Available Measurements
The data can be downloaded as compressed archives from the links below, or as individual files.
Sample plots of selected quantities are available.
The file couette.dat contains
- Profiles at \(x = 0.0\), \(0.175\), \(0.35\), \(0.525\), \(0.7\), \(0.875\), \(1.05\) and \(1.225\) m of:
- First order moments: \(U/U_b\), \(V/U_b\), \(U/U^*\)
- Second order moments: \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{u^2}/(U^*)^2\)
- Friction velocity (\(U^*\)) along the wavy wall at the above eight \(x\) locations.
Recommendations for Calculations
The following suggestions were given to contributors to a collaborative workshop in which the case was studied.
Inlet and Outlet Conditions
Ideally the calculation of the channel flow should be performed using periodicity conditions for both velocities and pressure gradient (\(dp(x+L)/dx = dp(x)/dx\)). However, given the short length of the experimental set-up, this may not be fully periodic, and it is therefore also possible to start at \(x = 0\), prescribing the experimental values provided as inlet conditions, and assume zero gradients for the flow variables at outlet.
References
- Nakabayashi, K., Kitoh, O., Iwata, H. (1991). Turbulent Couette type flow with an alternating pressure gradient. Proc. 8th Int. Symp. on Turbulent Shear Flows, Munich.
- El Telbany, M.M.M., Reynolds, A.J. (1980). Velocity distributions in plane turbulent channel flows. J. Fluid Mech., Vol. 100, pp. 1-29.
- Huffman, G.D., Bradshaw P. (1972). A note on von Kármán's constant in low Reynolds number turbulent flows. J. Fluid Mech., Vol. 53, pp. 45-60.
- Townsend, A.A. (1961). Equilibrium layers and wall turbulence. J. Fluid Mech., Vol. 11, pp. 97-120.
Indexed data:
| case010 (dbcase, confined_flow) | |
|---|---|
| case | 010 |
| title | Couette Flow with Fixed Wavy Wall |
| author | Nakabayashi, Kitoh, Iwata |
| year | 1989 |
| type | EXP |
| flow_tag | 2d, varying_cross_section |