2D Model Hill Flows
Experiments by Almeida, Durao, Heitor
Description
Flows over 2D polynomial-shaped obstacle(s) mounted on a flat plate with recirculation region in their wake.
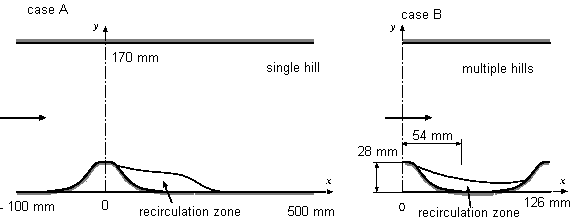
Two configurations are available, as shown in figure 1. In the first configuration, case \(A\), a single hill is mounted on the bottom of the channel. In the second one, case \(B\), a periodic flow is achieved over a series of consecutive hills mounted at the same location. The channel height is \(H = 170\) mm and the maximum height and length of each hill are respectively \(h_{max} = 28\) mm and \(2R = 108\) mm. In the case of consecutive hills, the space between each of them is \(4.5h_{max}\).
The shape of the hills was to be the inverse of a fourth-order polynomial but the actual shape is a little different. The actual height \(h(x)\) of the two-dimensional hills, in the form of a series of spline curves, are stored in file geom.dat.
Flow Characteristics
The hills are located about 6 m downstream of the tunnel inlet where a fully-developed channel flow is achieved in the absence of the obstacle(s). In case A, the measurements have been made around a single hill and, in case B, between two consecutive hills (the 7th and the 8th) located within an array of 10 equally spaced hills. The flow separates in the region of unfavourable pressure gradient on the downstream surface of the hills and, in the case of multiple hills, reattaches at an oblique angle on the upstream surface of the next hill. Very high levels of velocity fluctuations have been measured in the shear layers surrounding the recirculation bubbles.
Flow Parameters
- Water with a kinematic viscosity: \(\nu = 1\times 10^{-6}\) m2/s.
- Mean centreline velocity at inlet: \(U_o = 2.147\) m/s.
- Reynolds number: \(U_oh/\nu = 60,000\).
Inflow Conditions
Measurements are provided in file ch000.dat for a fully-developed channel flow in the absence of the hill(s):
- First order moment: \(U\)
- Reynolds stresses: \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\), \(\overline{uv}\)
The centreline turbulence intensity is about 3%, the friction factor is \(C_f = 0.0027\) and the wall friction velocity is \(u_{\tau} = 0.079\) m/s.
Measurement Techniques
Velocity measurements have been carried out using a Laser-Doppler Velocimeter up to 2 mm from the surface of the hill(s) and the bottom of the channel.
Measurement Errors:
For a 95% confidence level:
- \(\delta(\text{Mean values})\) : 0.5%
- \(\delta(\text{Reynolds stresses})\) : 3%
Available Measurements
The following profiles are available at 15 locations in case A (files <tt>1h*.dat</tt>) and 11 locations in case B (files <tt>2h*.dat</tt>).
Profiles of:
- First order moments: \(U\), \(V\)
- Reynolds stresses: \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{uv}\)
Sample plots of selected quantities are available.
The files can be downloaded individually, or compressed archives of all data files may be downloaded in the formats:
| Multiple hills | |||||
|---|---|---|---|---|---|
| \(x\) (mm) | \(U\) | \(V\) | \(\overline{u^2}\) | \(\overline{v^2}\) | \(\overline{uv}\) |
| 0 | 2b1umx00.dat | 2b1vmx00.dat | 2b1uux00.dat | 2b1vvx00.dat | 2b1uvx00.dat |
| 15 | 2b1umx01.dat | 2b1vmx01.dat | 2b1uux01.dat | 2b1vvx01.dat | 2b1uvx01.dat |
| 20 | 2b1umx02.dat | 2b1vmx02.dat | 2b1uux02.dat | 2b1vvx02.dat | 2b1uvx02.dat |
| 30 | 2b1umx03.dat | 2b1vmx03.dat | 2b1uux03.dat | 2b1vvx03.dat | 2b1uvx03.dat |
| 50 | 2b1umx04.dat | 2b1uux04.dat | 2b1vvx04.dat | 2b1uvx04.dat | |
| 63 | 2b1umx05.dat | 2b1vmx05.dat | 2b1uux05.dat | 2b1vvx05.dat | 2b1uvx05.dat |
| 76 | 2b1umx06.dat | 2b1uux06.dat | 2b1vvx06.dat | 2b1uvx06.dat | |
| 91 | 2b1umx07.dat | 2b1uux07.dat | 2b1vvx07.dat | 2b1uvx07.dat | |
| 96 | 2b1umx08.dat | 2b1vmx08.dat | 2b1uux08.dat | 2b1vvx08.dat | 2b1uvx08.dat |
| 116 | 2b1umx09.dat | 2b1vmx09.dat | 2b1uux09.dat | 2b1vvx09.dat | 2b1uvx09.dat |
| 126 | 2b1umx10.dat | 2b1uux10.dat | 2b1vvx10.dat | 2b1uvx10.dat | |
Recommendations for Calculations
Upper Wall: In both cases, the computational domain should extend to the upper wall of the channel, \(y = H = 170\) mm.
Case A: Single Hill
Inlet Conditions: The calculation of the channel flow should be started well upstream of the station \(x = -50\) mm (where the flow is influenced by the presence of the hill), using the experimental values provided as inlet conditions. Starting at \(x=-100\) mm is believed to be sufficient.
Outlet Conditions: The outlet section should be placed sufficiently far downstream of the single hill (\(x > 500\) mm) to assume zero streamwise gradients for the flow variables.
Case B: Consecutive Hills
Periodicity: Ideally the calculation of the channel flow should be performed using periodicity conditions for the flow variables.
Previous Numerical Studies
The case was considered at the 4th ERCOFTAC/IAHR Workshop on Refined Flow Modelling, held at Karlsruhe in 1995. A report on some of the reference solutions obtained for that workshop by researchers at UMIST and EDF for the single hill case, using \(k\)-\(\varepsilon\) and stress-transport models, is available as hillflow.pdf.
Main References
- Almeida, G.P., Durao, D.F.G., Heitor, M.V. (1992). Wake flows behind two dimensional model hills. Exp. Thermal and Fluid Science, Vol. 7, p. 87.
- Almeida, G.P., Durao, D.F.G., Simoes, J.P., Heitor, M.V. (1990). Laser-Doppler measurements of fully developed turbulent channel flow. Proc. 5th Symp. Appl Laser Techniques to Fluid Mech., pp. 5-12.
- Hunt, J.C.R., Snyder, W.H. (1980). Experiments on stably and neutrally stratified flow over a model three-dimensional hill. J. Fluid Mech., Vol. 96, pp. 671-704.
- Castro, J.P., Haque, A. (1987). The structure of a turbulent shear layer bounding a separation region. J. Fluid Mech., Vol. 179, pp. 439-468.
Indexed data:
| case018 (dbcase, confined_flow) | |
|---|---|
| case | 018 |
| title | 2D Model Hill Flows |
| author | Almeida, Durao, Heitor |
| year | 1992 |
| type | EXP |
| flow_tag | 2d, separated, varying_cross_section |