Boundary Layer In and Downstream from Convex Curvature
Experiment by Alving, Smits, Watmuff
Description
Developing boundary layer submitted to stabilizing convex curvature at \(Re_{\theta} = 6000\) without longitudinal pressure gradient (\(S = \partial p/\partial x \approx 0\)).
A study to examine the flat plate relaxation behaviour of a turbulent boundary layer recovering from 90o of strong convex curvature (\(\delta_o/R = 0.08\)), for a length of approximately \(90\delta_o\) after the end of curvature, where \(\delta_o\) is the boundary layer thickness at the start of the curvature.
Geometry
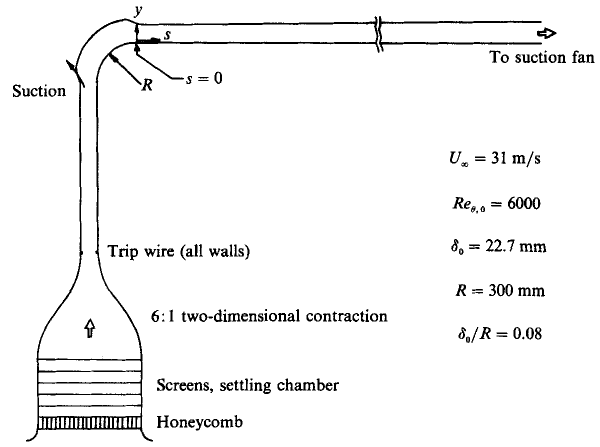
The experimental facility used to obtain the results was a subsonic, open-return wind tunnel as shown in figure 1.
As is shown by the schematic, the flow first passes through a honeycomb and a set of screens at the entrance to the wind tunnel. The flow is then subjected to a 6:1 two-dimensional contraction. A 1.0 mm diameter wire was then used to trip the boundary layer on all four walls of the 0.15 m \(\times\) 1.22 m working section. At a distance of 1.5m downstream of the trip, the boundary layer was subjected to a 90o constant radius strong convex curvature with \(R = 300\) mm. To isolate curvature effects from those due to pressure gradient, the wall opposite the test wall was contoured to minimize the test-wall pressure gradient. The boundary layer on the outer wall of the curved section was removed by suction to prevent separation. The presence of this bend introduced a source of secondary flow from the sidewall boundary layers. The effect of these boundary layers was minimized by the use of high-momentum, low mass flow rate, jets located on the side walls near to the beginning of the curvature.
The test wall boundary layer was then allowed to relax over a section of flat plat in zero pressure gradient conditions. The length of this section, \(s\), was 4.9m as measured from the exit from the curved section.
Inflow Conditions
The test wall boundary layer developed in a zero pressure gradient with a freestream velocity of 31 m/s and a free stream turbulence intensity of 0.3%.
At the start of the bend, 1.5 m downstream of the trip, the boundary layer had a Reynolds number based on momentum thickness \(Re_{\theta}\) of 6000. The value of \(\delta_o\) at this point was 22.7 mm.
Flow Characteristics
The flow during this study can be broken down into three distinct stages, before, during and after the 90o convex curvature.
During the first stage, before the curved section, a turbulent boundary layer is generated. The boundary layer generated on the wall opposite the test wall was removed to prevent separation. The flow is then subjected to 90o of constant-radius convex curvature (\(R = 300\) mm). The test wall boundary layer is then allowed to relax on a flat plate. Since this case is limited to the relaxation of the boundary layer, it concentrates on the characteristics of the flow downstream of the curvature.
Mean Flow Characteristics
The first aspect of the flow described is the recovery behaviour of the skin friction. At the exit to the bend, the skin friction values are low, reflecting the stabilizing influence of the convex curvature. Once the curvature is removed, the skin friction begins to recover quite quickly, doubling within \(10\delta_o\). The recovery rate then decreases, but \(C_f\) continues to increase through most of the recovery. In the early stages of recovery, the boundary layer is obviously far from equilibrium, but in the later stages (\(s/\delta_o > 25\)), the measured skin friction appears to approach the flat plate correlations asymptotically.
The next aspect to be considered is the mean velocity profiles. At the bend exit, the effect of the boundary-layer perturbations is shown by the short extent of the logarithmic region and by the large wake factor (see figure 7 in Alving et al, 1990). Once the curvature is removed the velocity profile initially changes quickly; between the two stations at \(s/\delta_o = 2\) and \(4\), the wake factor decreases by 50%. The recovery rate remains high for the first \(10\delta_o\). As the recovery continues, the Coles wake factor asymptotically approaches a constant level slightly above that of the upstream reference level, (0.76 compared with 0.68).
All of the boundary layer thicknesses (boundary layer, displacement and momentum) increase through the bend and then dip during the initial recovery region. During the first approximately \(10\delta_o\) after the end of curvature, the shape factor \(H\) and Clauser parameter \(G\) recover to 75% of their flat plate values. The levels of \(H\) and \(G\) then recover to near to their flat plate values (1.35 and 7.54 compared to 1.4 and 7.53), but at a much slower rate.
Turbulent Characteristics
The turbulent characteristics of the flow can be broken down into three stages of recovery.
During the first stage of recovery, the initial re-growth of the turbulence levels suppressed by the curvature occur through a stress bore which is generated near the wall and is carried outward by turbulent transport. In spite of the distortion this bore causes in the absolute stress levels, the various stresses change in a similar manner; therefore the stress ratios are not severely perturbed and they recover quickly and monotonically.
During the second stage of recovery, the stress bore has grown to fill the entire shear layer. However, the stress levels continue to rise, at a decreased rate, above the upstream levels.
The third stage of recovery is marked by a drop in the stress levels, but the recovery rate is so slow that only a slight difference is measured over the last \(23\delta_o\) of the test section, indicating a much longer relaxation length would be required to complete recovery.
After a distance of \(87\delta_o\) beyond the end of curvature, the boundary layer is still quite different from the upstream self-preserving layer, both in the magnitude and distribution of the turbulent stresses. This indicates that a very long relaxation length would be required to complete recovery, and is in complete contrast to the mean flow behaviour which does not look significantly different from the unperturbed case.
Experimental Details
The total pressure in the boundary layer was measured using a circular Pitot tube of 1.0 mm. Skin friction was measured with Preston probes of diameter 1.0, 1.6 and 2.4 mm.
One-point turbulence measurements were taken using DANTEC 55P05 (normal-wire boundary layer) and 55P51 (crossed-wire) probes. The probes were modified so that the active wire lengths were reduced to 0.75mm and the spacing between crossed wires was reduced to 0.4mm to minimize spatial resolution difficulties.
Multiple point turbulence measurements were made using a probe consisting of eight normal wires (of which six were used) spaced 0.5 to 1.0mm apart in the direction normal to the wall, resulting in a total span of 5.5mm. The possible blockage effects of the probe having a large cross-sectional area and the tip being only 25mm upstream of the shaft were found to be small.
DANTEC 55D01 and 55M10 constant-temperature anemometers were used, operating at overheat ratios of 0.7 with frequency responses of at least 65 kHz. The signals were filtered at 25 kHz with a fourth-order Butterworth filter. The one point measurements were digitized at 2.5 and 50 kHz with a 12 bit A/D converter. The data taken at the lower frequency were used for long- time averages, while the higher frequency data were used for spectral decomposition. The rake data were digitized at 250 kHz using a 10 bit A/D converter.
For all of the one point measurements, the wires were calibrated using a dynamic calibration scheme as described by Perry (1982) and modified by Watmuff (1979) and Alving (1988).
Measurement Errors
There appears to be generally good agreement among the various estimates of \(C_f\), although there are two exceptions to this which are worth discussing.
Firstly, there is some scatter in the initial recovery region. This may be expected, since the Preston probe calibration is affected by pressure gradients. Patel (1965) correlated the errors in the inferred skin friction using the pressure gradient parameter \(\Delta\), where:
\[ \Delta=(\nu/\rho_r^3) \frac{dp}{ds} \]
Between \(s/\delta_o = 4\) and \(10\), \(\Delta\) was estimated at -0.006 or 0.007, and Patel's calibration suggests \(C_f\) is over-estimated by 6% in this region. In the rest of the recovery, the pressure gradient was negligible.
Other than in the initial recovery region, the skin friction results only show scatter around \(s/\delta_o = 65-70\). These measurements were retaken several times, without discovering the source of the discrepancy. One potential source of this discrepancy could be the slight favourable pressure gradient at this measuring station. The Reynolds stress behaviour also shows an anomaly which may be due to this small pressure gradient.
Available Measurements
Data are provided at nine locations (one in the boundary layer upstream of the curved section and eight in the recovery section downstream of the bend). The data consists of:
- Pressure coefficient measurements along the wall.
- Pitot tube measurements of mean velocity profiles at each of the nine location.
- Single- and cross-wire hot wire measurements of mean velocity, Reynolds stresses and triple moments at most of the nine locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt contains a description of the files and data formats.
info.dat contains a summary of \(C_f\), \(C_p\) and wall friction velocity values at each measurement station.
cp1.dat and cp2.dat contain pressure coefficient measurements along the wall.
The mean velocity and higher moment profiles are available as in the table below.
| Location | Pitot survey data | Single wire data | U-V cross wire data | U-W cross wire data |
|---|---|---|---|---|
| 1 (\(s=-0.771\) m) | p1mean.dat | p1u.dat | p1uv.dat | p1uw.dat |
| 2 (\(s=0.021\) m) | p2mean.dat | |||
| 3 (\(s=0.102\) m) | p3mean.dat | p3u.dat | p3uv.dat | p3uw.dat |
| 4 (\(s=0.243\) m) | p4mean.dat | p4u.dat | p4uv.dat | p4uw.dat |
| 5 (\(s=0.393\) m) | p5mean.dat | p5u.dat | p5uv.dat | p5uw.dat |
| 6 (\(s=0.674\) m) | p6mean.dat | p6u.dat | p6uv.dat | p6uw.dat |
| 7 (\(s=0.974\) m) | p7mean.dat | p7u.dat | p7uv.dat | p7uw.dat |
| 8 (\(s=1.475\) m) | p8mean.dat | p8u.dat | p8uv.dat | p8uw.dat |
| 9 (\(s=1.975\) m) | p9mean.dat | p9u.dat | p9uv.dat | p9uw.dat |
References
- Alving, A.E., Smits, A.J., Watmuff, J.H. (1990). Turbulent boundary-layer relaxation from convex curvature. J. Fluid Mech., Vol. 211, pp. 529-556.
- Alving, A.E. (1988). Boundary layer relaxation from curvature. PhD thesis, Princetown Univ.
- Smits, A.J., Alving, A.E., Smith, R.W., Spina, E.F., Fernando, E.M., Donovan, J.F. (1989). A comparison of the turbulence structure of subsonic and supersonic boundary layers. Physics of Fluids, Vol. 11, pp. 1865-1875.
- Perry, A.E. (1982). Hot-wire Anemometry. Oxford University Press.
- Watmuff, J.H. (1979). Phase-averaged large scale structures in three-dimensional turbulent wakes. PhD thesis, University of Melbourne, Melbourne, Australia.
- Patel, V.C. (1965). Calibration of the Preston tube and limitations on its use in pressure gradients. J. Fluid Mech., Vol. 23, pp. 185-208.
Indexed data:
| case022 (dbcase, confined_flow) | |
|---|---|
| case | 022 |
| title | Boundary Layer in and Downstream from Convex Curvature |
| author | Alving, Smits, Watmuff |
| year | 1990 |
| type | EXP |
| flow_tag | 2d, curvature |