Normally-Impinging Jet from a Circular Nozzle
Experiments by Cooper, Jackson, Launder, Liao, and Baughn and Shimizu
Description
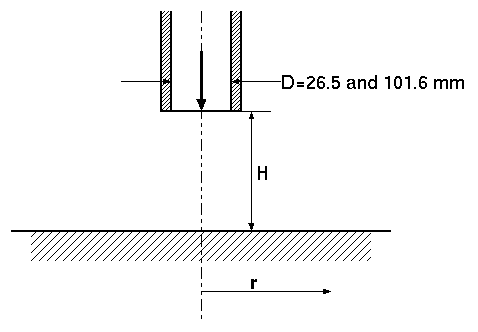
The experiments provide an extensive set of measurements of a circular turbulent jet impinging orthogonally onto a large plane surface, as shown in figure 1. Two Reynolds numbers have been considered, \(2.3\times 10^4\) and \(7\times 10^4\), while the height of the jet discharge above the plate ranges from two to ten diameters, with particular attention focused on two and six diameters. The experiment for the velocity field was designed so that it provided hydrodynamic data for conditions the same as those employed by Baughn & Shimizu (1989) and Baughn et al (1992) when measuring heat-transfer rates. Before discharge, the air passed along a smooth pipe sufficiently long to give fully developed flow at the exit plane of the jet: a feature that is helpful in using the data for turbulence-model evaluation. Hot-wire measurements have been made for cases with jet inlet pipes of nominally one-inch (26 mm) and four inches (101.6 mm) diameter. Data are available of the mean velocity profile in the vicinity of the plate surface and also of the three Reynolds-stress components lying in the \(x-r\) plane. Computational results reported in Craft et al (1993) indicate a good degree of internal consistency between the mean and turbulent field data in that models predicting the mean flow poorly (or well) also predict the turbulence data poorly (well).
Inlet and Boundary Conditions
As noted above, at the pipe exit, the flow should be fully-developed. In computational work, it is suggested that an initial calculation should be done to generate fully-developed pipe flow profiles at the appropriate Reynolds number, which can then be used as inlet conditions for the impinging jet computation.
The outlet plane should be placed at a sufficiently large radial distance that errors arising from the application of zero-gradient (or similar) conditions will not significantly affect the region of interest. For the present measurements (extending to around \(r/D=6\)), it is suggested that the outer radial boundary should be at \(r/D=8\) or greater.
The boundary opposite the impingement wall is a surface across which fluid in entrained. One common method of dealing with such boundaries (in pressure-correction based finite-volume solvers) is to impose ambient pressure values at the boundary, and to allow fluid to be entrained at the rate necessary to satisfy continuity in the boundary cells.
Measurement Techniques
Apparatus and Instrumentation
The experiments were carried out with two different pipe configurations. The first series employed a copper pipe of 1.025 in (26 mm) internal diameter, 2.1 m in length giving a length:diameter ratio of 80:1. Air was supplied from a centrifugal blower via flexible tubing. At the inlet to the copper tube, a flow-straightening honeycomb was fitted in the form of drinking straws glued together. The flow rate through the pipe was controlled by a bleed valve. The second series employed a 4 in. (101.6 mm) diameter brass pipe 81 diameters in length. This was preceded by a further section of slightly smaller diameter pipe (99 mm) giving a total run of 12.5 m or 125 diameters. In this case the flow entered the pipe by way of a contracting section and the air supply rate was controlled by a variable speed d.c. fan.
The rectangular test plate on which the flow impinged, measuring \(1275\times 975\) mm, was made from printed-circuit board fixed to a 25 mm thick plywood backing.
Measurements in the impinging jet were made with a TSI IFA-100 two-channel hot-wire anemometer interfaced to a data acquisition system.
Measurement Errors
Before the test programme proper began, extensive validation checks were made to ensure the flow's symmetry. For this purpose, profile measurements were made at intervals around the jet for different normalised jet heights (\(H/D\)) and radius ratios (\(r/D\)). The results of these tests indicated that the profiles at different angular positions were indistinguishable from one another.
The experimental programme has covered height:diameter ratios of 2, 3, 4, 6 and 10 though the greatest emphasis has been given to the case where \(H/D = 2\) as this represents both the easiest case to simulate numerically and is one for which heat transfer data (Baughn & Shimizu, 1989) are available. For the 26 mm diameter pipe, measurements extended up to \(r/D = 9\) and for the larger diameter pipe to \(r/D = 3\), the latter limit being set partly by the lower velocities and partly to avoid 'edge' effects. Measurements in the smaller pipe were made at a nominal Reynolds number of \(2.3\times 10^4\) only, while, in the larger pipe, at Reynolds numbers of \(2.3\times 10^4\) and \(7.1\times 10^4\). However, in this larger pipe, at the lower Reynolds number, only the two smallest values of \(H/D\) were considered. There is thus a reasonable degree of overlap between the experiments in the two pipes and a satisfactory level of accord was found to exist between the two sets.
While both single- and cross-wire measurements were taken with both pipes, only those obtained with the larger pipe are reported here due to the thinness of the wall jet in the case of the smaller pipe. For every position in the velocity traverse ten batches of 512 data points per wire were recorded, the points in each batch being gathered at 100 samples per second with a short interval between each batch. The mean and r.m.s. values of velocity and the mean cross-correlation were evaluated from these 5120 data points.
Absolute accuracies of the data are difficult to assess and, indeed, vary greatly across the flow. However, the maximum mean velocity at any position relative to the bulk velocity is believed to be accurate within +/- 2%. Root-mean-square fluctuating velocities have a corresponding estimated uncertainty of +/- 4% (\(u'\)) and +/- 6% (\(v'\)) for values of \(y\) less than \(y_{1/2}\), while turbulent shear-stress (\(\overline{uv}\)) uncertainties are typically of the order of +/- 9% except near the jet impingement point and other regions where the correlation coefficient \(\overline{uv}/(u' v')\) is smaller than about 0.2. There are two other indications of the data's internal consistency: the rate of growth of the impinging jet for \(H/D = 10\) corresponds closely with the asymptotic growth of the radial wall jet while, as Craft e al (1993) shows, turbulence models displaying best accord with the mean velocity also achieve the best agreement with the turbulence field.
Available Measurements
Measurements of mean velocity, normal stresses \(\overline{u^2}\) and \(\overline{v^2}\) and turbulent shear stress \(\overline{uv}\) are available at a number of radial locations up to \(r/D=3\). Heat transfer measurements, in the form of Nusselt number as a function of radial position \(r/D\), are also available.
Sample plots of selected quantities are available.
Individual files, containing mean velocity \(U\) and \(\overline{u^2}\) measured with a single wire probe; \(\overline{v^2}\) and shear stress \(\overline{uv}\) measured with a cross-wire probe, and Nusselt number, are available in the files detailed in the tables below. Note that since \(U\) and \(\overline{u^2}\) are measured with a single wire, they represent the velocity and normal stress in the streamwise direction. They thus correspond to the wall-normal velocity and stress along the stagnation line at \(r/D=0\), but the velocity and stress parallel to the wall at large \(r/D\) values, where the flow resembles a radial wall jet. The \(\overline{v^2}\) data represents the wall-normal stress.
The data can be downloaded as compressed archives from the links below, or as individual files.
| \(H/D=2\), \(Re=23000\) | ||||
|---|---|---|---|---|
| \(r/D\) | \(U\) | \(\overline{u^2}\) | \(\overline{v^2}\) | \(\overline{uv}\) |
| 0.0 | ij2lr-00-sw-mu.dat | ij2lr-00-sw-uu.dat | ||
| 0.5 | ij2lr-05-sw-mu.dat | ij2lr-05-sw-uu.dat | ij2lr-05-cw-vv.dat | ij2lr-05-cw-uv.dat |
| 1.0 | ij2lr-10-sw-mu.dat | ij2lr-10-sw-uu.dat | ij2lr-10-cw-vv.dat | ij2lr-10-cw-uv.dat |
| 1.5 | ij2lr-15-sw-mu.dat | ij2lr-15-sw-uu.dat | ||
| 2.0 | ij2lr-20-sw-mu.dat | ij2lr-20-sw-uu.dat | ||
| 2.5 | ij2lr-25-sw-mu.dat | ij2lr-25-sw-uu.dat | ij2lr-25-cw-vv.dat | ij2lr-25-cw-uv.dat |
| 3.0 | ij2lr-30-sw-mu.dat | ij2lr-30-sw-uu.dat | ij2lr-30-cw-vv.dat | ij2lr-30-cw-uv.dat |
| \(Nu\) | ij2lr-nuss.dat | |||
| \(H/D=2\), \(Re=70000\) | ||||
|---|---|---|---|---|
| \(r/D\) | \(U\) | \(\overline{u^2}\) | \(\overline{v^2}\) | \(\overline{uv}\) |
| 0.0 | ij2hr-00-sw-mu.dat | ij2hr-00-sw-uu.dat | ||
| 0.5 | ij2hr-05-cw-vv.dat | ij2hr-05-cw-uv.dat | ||
| 1.0 | ij2hr-10-sw-mu.dat | ij2hr-10-sw-uu.dat | ij2hr-10-cw-vv.dat | ij2hr-10-cw-uv.dat |
| 1.5 | ij2hr-15-sw-mu.dat | ij2hr-15-sw-uu.dat | ij2hr-15-cw-vv.dat | ij2hr-15-cw-uv.dat |
| 2.0 | ij2hr-20-sw-mu.dat | ij2hr-20-sw-uu.dat | ij2hr-20-cw-vv.dat | ij2hr-20-cw-uv.dat |
| 2.5 | ij2hr-25-sw-mu.dat | ij2hr-25-sw-uu.dat | ij2hr-25-cw-vv.dat | ij2hr-25-cw-uv.dat |
| 3.0 | ij2hr-30-sw-mu.dat | ij2hr-30-sw-uu.dat | ij2hr-30-cw-vv.dat | ij2hr-30-cw-uv.dat |
| \(Nu\) | ij2hr-nuss.dat | |||
| \(H/D=6\), \(Re=23000\) | ||
|---|---|---|
| \(r/D\) | \(U\) | \(\overline{u^2}\) |
| 0.0 | ij6lr-00-sw-mu.dat | ij6lr-00-sw-uu.dat |
| 0.5 | ij6lr-05-sw-mu.dat | ij6lr-05-sw-uu.dat |
| 1.0 | ij6lr-10-sw-mu.dat | ij6lr-10-sw-uu.dat |
| 1.5 | ij6lr-15-sw-mu.dat | ij6lr-15-sw-uu.dat |
| 2.0 | ij6lr-20-sw-mu.dat | ij6lr-20-sw-uu.dat |
| 3.0 | ij6lr-30-sw-mu.dat | ij6lr-30-sw-uu.dat |
| \(Nu\) | ij6lr-nuss.dat | |
| \(H/D=6\), \(Re=70000\) | ||||
|---|---|---|---|---|
| \(r/D\) | \(U\) | \(\overline{u^2}\) | \(\overline{v^2}\) | \(\overline{uv}\) |
| 0.0 | ij6hr-00-sw-mu.dat | ij6hr-00-sw-uu.dat | ||
| 0.5 | ij6hr-05-sw-mu.dat | ij6hr-05-sw-uu.dat | ij6hr-05-cw-vv.dat | ij6hr-05-cw-uv.dat |
| 1.0 | ij6hr-10-sw-mu.dat | ij6hr-10-sw-uu.dat | ij6hr-10-cw-vv.dat | ij6hr-10-cw-uv.dat |
| 1.5 | ij6hr-15-sw-mu.dat | ij6hr-15-sw-uu.dat | ij6hr-15-cw-vv.dat | ij6hr-15-cw-uv.dat |
| 2.0 | ij6hr-20-sw-mu.dat | ij6hr-20-sw-uu.dat | ij6hr-20-cw-vv.dat | ij6hr-20-cw-uv.dat |
| 2.5 | ij6hr-25-sw-mu.dat | ij6hr-25-sw-uu.dat | ij6hr-25-cw-vv.dat | ij6hr-25-cw-uv.dat |
| 3.0 | ij6hr-30-sw-mu.dat | ij6hr-30-sw-uu.dat | ij6hr-30-cw-vv.dat | ij6hr-30-cw-uv.dat |
| \(Nu\) | ij6hr-nuss.dat | |||
Reference and Previous Solutions
The impinging jet flow is a particularly challenging case for turbulence models. The stagnation region flow is dominated by normal straining of the fluid and, as will be noted below, many of the widely-used models which have been developed primarily for shear flow boundary layers fail to predict the response of the turbulence to normal straining.
Craft et al (1993) reported predictions of the flow using four different turbulence models. They concluded that standard linear eddy-viscosity models significantly overpredict turbulence energy levels (and thus heat-transfer rates) in the stagnation region, as a result of the linear Boussinesq stress-strain relation mis-representing the normal stresses and leading to excessive turbulence energy generation rates. When a non-linear eddy-viscosity model which can correctly represent the normal stresses is employed, Craft et al (1996) shows that the overprediction of turbulence energy and heat-transfer can be avoided. Durbin (1996) also managed to avoid excessive turbulence energy levels by essentially employing a strain-rate dependent limiter on the turbulent viscosity, which prevents the predicted normal stress anisotropy from becoming too large.
Craft et al (1993) also reported predictions employing stress-transport models. They showed that the linear IP model, when used in conjunction with the wall-reflection terms of Gibson & Launder (1978), gave results little better than the linear EVM. This failure was due to the form of the wall-reflection terms, which were developed by considering flow parallel to a wall, and actually have the effect of increasing the stress normal to the wall in impinging flow. When these were replaced with the proposal of Craft & Launder (1992) (which were designed to predict flows both parallel and normal to a wall), reasonable predictions were obtained.
The case has been studied in two ERCOFTAC/IAHR Workshops on Refined Turbulence Modelling, held at Ecole Centrale de Lyon in October 1991, and at UMIST in 1993.
References and Related Publications
- Cooper, D., Jackson, D.C., Launder, B.E., Liao, G.X. (1993). Impinging jet studies for turbulence model assessment. Part I: Flow-field experiments. Int. J. Heat Mass Transfer, Vol. 36, pp. 2675-2684.
- Baughn, J.W., Yan, X., Masbah, M. (1992). The effect of Reynolds number on the heat transfer distribution from a flat plate to an impinging jet. ASME Winter annual meeting.
- Baughn, J.W., Shimizu, S. (1989). Heat transfer measurement from a surface with uniform heat flux and an impinging jet. ASME J. of Heat Transfer, Vol. 111, pp. 1096-1098.
- Craft, T.J., Graham, L.J.W., Launder, B.E. (1993). Impinging jet studies for turbulence model assessment. Part II: An examination of the performance of four turbulence models. Int. J. Heat Mass Transfer, Vol. 36, pp. 2685-2697.
- Craft, T.J., Launder, B.E., Suga, K. (1996). Development and application of a cubic eddy-viscosity model of turbulence. Int. J. Heat and Fluid Flow, Vol. 17, pp. 108-115.
- Durbin, P.A. (1996). On the \(k\)-3 stagnation point anomaly. Int. J. Heat Fluid Flow, Vol. 17, pp. 89-90.
- Gibson, M.M., Launder, B.E. (1978). Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech., Vol. 86, p. 491.
- Craft, T.J., Launder, B.E. (1992). New wall-reflection model applied to the turbulent impinging jet. AIAA J., Vol. 30, pp. 2970-2972.
Indexed data:
| case025 (dbcase, semi_confined_flow) | |
|---|---|
| case | 025 |
| title | Normally Impinging Jet from a Circular Nozzle |
| author | Cooper, Jackson, Launder, Liao, Baughn, Shimizu |
| year | 1993 |
| type | EXP |
| flow_tag | axisymmetric, scalar, jet |