Infinite 35 Degree Swept Wing
Experiments by Van den Berg, Elsenaar, Lindhout, Wesseling
Description
This study was undertaken by the authors in order to investigate three-dimensional turbulent boundary layers. A two dimensional boundary layer initially developed on a test plate is subjected to adverse pressure gradient leading to three dimensional separation near the trailing edge of the plate.
Reynolds number \(Re_{\theta} = 3290\).
Geometry
In order to obtain a test set-up suitable for checking three-dimensional boundary-layer calculation methods, the following requirements were made of the experimental model.
- A flow similar to that which occurs on an infinite swept wing should be simulated.
- The pressure should be constant along the most forward part of the model, leading to the development of a two-dimensional constant pressure boundary layer. This means the initial conditions for the three-dimensional boundary layer are then well know.
- The measurements should be carried out in a boundary layer on a flat surface, to eliminate the effects of surface curvature on the structure of turbulence.
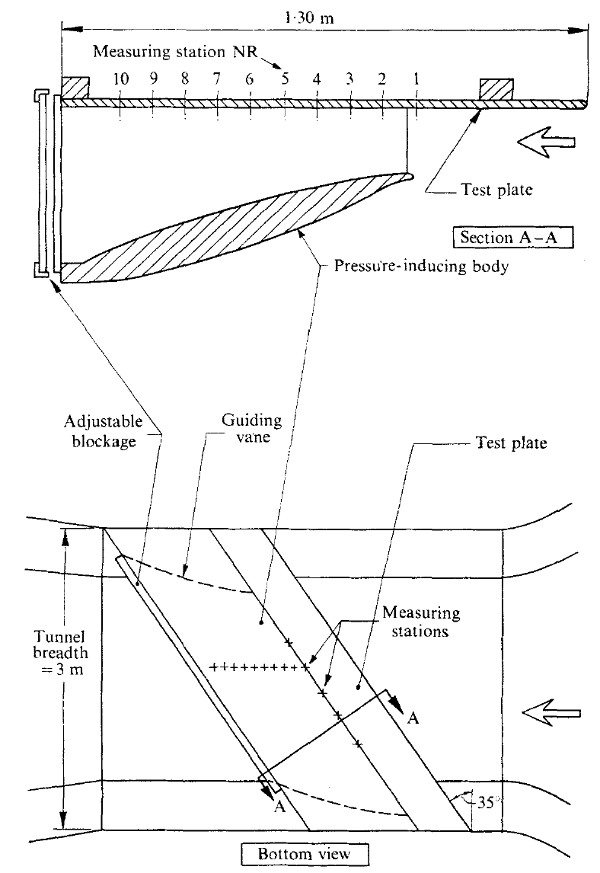
A sketch of the resulting model can be seen in figure 1.
The model consisted of a smooth flat plate with a pressure distribution induced on it by a large airfoil-like body mounted near the plate. Both the flat test plate and the pressure-inducing body had an angle of sweep of 35o.
In order to achieve the requirement of a constant pressure region along the forward part of the flat plate, a variable number of bars were placed at the channel outlet, allowing the correct amount of air to pass through the channel. Another feature of the model is the presence of guiding vanes mounted between the pressure-inducing body and the test plate, thus providing a reasonably close approximation to the infinite swept-wing condition.
The model was installed in the NLR 3m \(\times\) 2m low speed wind tunnel.
Flow Conditions/Parameters
The flow through the model consisted of three regimes. The first of these is a constant pressure, two-dimensional boundary layer which develops on the furthest upstream part of the model, (right hand edge of the diagram. The flow in front of the diverging region should be parallel to obtain the constant pressure region along the most forward part of the plate. The parallel flow was achieved by the use of a blockage in the channel.
To achieve the three dimensional separation near the model trailing edge, the pressure is required to increase in the direction of flow. This is achieved by creating a diverging channel flow. The use of the pressure inducing body, a large airfoil like body, mounted near to the plate, also swept at 35o (see diagram) provides the pressure increase in the direction of flow. The pressure rise should not be too steep as this reduces the value of such an experiment as a check on semi-empirical calculation methods. To diminish the influence of the end walls on the flow, curved guiding vanes were introduced, the shape of which were determined experimentally by trial and error so that the pressure distribution on the test plate approximated the infinite swept-wing condition as accurately as possible.
Measurement Techniques
To determine the pressure distribution on the test plate, the static pressure was measured at about 200 locations through holes in the surface of the plate. Such a large number of static pressure holes were required if the pressure gradients were to be deduced with sufficient accuracy.
The direction and magnitude of the velocity at the boundary layer edge were measured with a cylindrical yaw tube and a Pitot static tube, respectively. The velocity measurements inside the boundary layer were carried out with a rotatable hot wire probe. The probes at the measuring stations were protruded through the plate surface. At the reverse side of the plate, a traversing mechanism was mounted, by which the probe could be translated and rotated. The measurements extended from outside the boundary layer up to a distance of 0.15mm from the surface. The direction of the velocity was found by rotating the hot wire and subsequently determining the line of symmetry of the data.
The hot wire was calibrated at the boundary layer edge, where the magnitude of the velocity is known from Pitot static tube measurements. Calibrations were made before and after each traverse through the boundary layer. The traverse was repeated when the difference between both calibrations was larger than 1% in the mean velocity.
The magnitude of the wall shear stress was determined by wall Pitots of the Stanton type, with slit heights of 0.1mm and 0.2mm. Both wall Pitots were calibrated in a long pipe with fully developed flow. The wall Pitots were rotated to establish the symmetry line, and thus the approximate direction of the wall shear stress. More details concerning the experimental techniques employed are given in van den Berg & Elsenaar (1972).
Numerical Techniques
For a summary of the numerical techniques employed in order to provide a comparison with experimental results, refer to van den Berg et al (1975).
Available Measurements
The available data consists of:
- Pressure coefficient distribution along the wall, and at a distance from it of \(y=75\) mm.
- Mean velocity and Reynolds stress profiles across the boundary layer at a number of streamwise locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
f0251a-pt1.dat Contains mean velocity profiles at nine locations: \(x= 0.52\), \(0.62\), \(0.72\), \(0.82\), \(0.92\), \(1.02\), \(1.12\), \(1.22\), \(1.32\) and \(1.42\) m.
f0251a-pt2.dat Contains Reynolds stress profiles at eight locations: \(x= 0.495\), \(0.795\), \(0.895\), \(0.995\), \(1.095\), \(1.195\), \(1.295\) and \(1.395\) m.
f0251a-pt3.dat Contains the distribution of static pressure coefficient along the flat plate wall, and along a line at \(y=75\) mm.
References
- Van Den Berg, B., Elsenaar, A. Lindhout, J.P.F., Wesseling, P. (1975). Measurements in an incompressible three dimensional turbulent boundary layer, under infinite swept-wing conditions, and comparison with theory. J. Fluid Mech., Vol. 70, p. 127.
- Van Den Berg, B., Elsenaar, A. (1972). NLR Tech. Rep. No. 72092 U.
Indexed data:
| case027 (dbcase, flow_around_body) | |
|---|---|
| case | 027 |
| title | Infinite 35 degree swept wing |
| author | Van den Berg, Elsenaar, Lindhout, Wesseling |
| year | 1975 |
| type | EXP |
| flow_tag | 3d, streamlined_body |