Pseudo-Ekman Boundary Layer
DNS by Spalart
Description
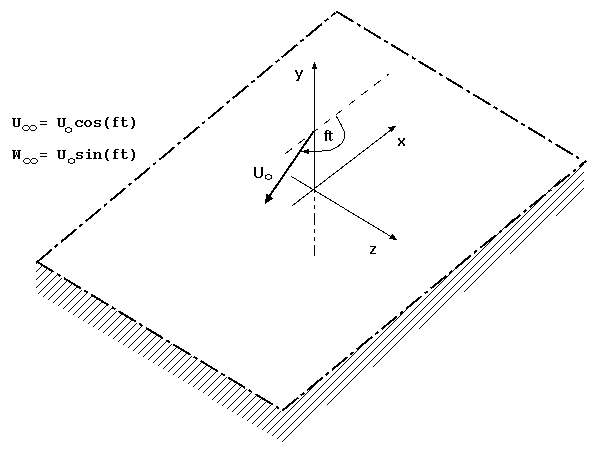
In this study, a three dimensional boundary layer is simulated on an infinite flat plate by a time dependent free-stream velocity vector, whose magnitude is independent of time but whose direction, as seen in plan view, changes at a constant angular velocity (see figure 1). A pressure gradient at right angles to the free-stream velocity induces a skewing of the velocity profile. The flow is studied theoretically using Reynolds number scaling laws and by direct numerical simulation over a range of Reynolds numbers.
Reynolds number: \(Re_1 = U_o(2/(f\nu))^{1/2} = 500\), \(620\) and \(767\) where \(U_o\) is the free-stream velocity magnitude and \(f\) the angular rate at which its direction rotates.
Geometry
The fluid domain is the half space \([-\infty,\infty]\times [0,\infty]\times [-\infty, \infty]\) in the \(x\), \(y\), \(z\) directions.
At the wall, \(y = 0\), the no slip condition applies so the velocity vector \((u, v, w) = 0\).
The grid spacing used was \(\Delta x^+ = \Delta z^+ \approx 7\), and in the \(y\) direction there were at least ten grid points within 10 wall units of the wall.
The grids had \(128\times 50\times 128\) grid points at a Reynolds number \(R_1 = 500\); \(192\times 64\times 192\) grid points at \(R_1 = 620\), and \(256\times 80\times 256\) grid points at \(R_1 = 767\). During the establishment of the flow, a coarser grid was used; halving the number of points in each direction reduces the computer cost per time unit by a factor of about 20.
Simulations on such coarse grids produce acceptable large eddies but are not accurate enough near the wall, since they may overpredict the friction coefficient by as much as 20% at a given Reynolds number. With a spectral method it is a simple matter to interpolate from one grid to another; the interpolation is often done in steps, for instance from 128 points to 192 and then to 256 for the 'true' simulation.
Inflow Conditions
The initial conditions were the sum of the laminar profile and random disturbances of finite amplitude, typically +/-20% of \(U_o\). Since only the turbulent state is of interest there is no point in starting from small disturbances (in addition, the turbulence appears to be subcritical). When available, the final state of a lower-Reynolds number simulation was used as the initial condition.
The only variable parameter in this analysis was the Reynolds number.
Flow Characteristics
In the free stream, as \(y\) tends to infinity, the velocity vector is prescribed as a function of time, but is independent of \(x\) and \(z\):
\[ U_{\infty} = U_o\cos(ft) \] \[ W_{\infty} = U_o\sin(ft) \]
The velocity vector describes a circle of radius \(U_o\), centred at (0,0), and rotates at an angular rate \(f\). The vorticity is zero outside the boundary layer.
Inside the domain, the incompressible Navier-Stokes equations apply. Disregarding the initial conditions, this problem only has three parameters, the velocity \(U_o\), the frequency \(f\) and the kinematic viscosity \(\nu\). The thickness of the laminar solution is:
\[ \delta_l = \left(2\nu/f\right)^{1/2} \]
The parameters combine into a single non-dimensional parameter, the Reynolds number:
\[ Re_l = \frac{U_o\delta_l}{\nu} = U_o \left(\frac{2}{f\nu}\right)^{1/2} \]
In this study, solutions which are statistically homogeneous in \(x\) and \(z\) are being sought. The solutions were therefore run for long enough to lose the memory of the initial conditions. If the flow is laminar, the large time solution is periodic:
\[ U = U_o \left[ \cos(\phi) - e^{-y/\delta_l} \cos(\phi-y/\delta_l)\right] \qquad V=0 \qquad W = U_o \left[ \sin(\phi) e^{-y/\delta_l} \cos(\phi-y/\delta_l)\right] \]
If the flow is turbulent, we expect the statistics to be time periodic as opposed to a behaviour where quantities such as displacement thickness grow indefinitely. This is because the symmetry of the free-stream motion precludes the accumulation of momentum in any one particular direction.
The equations and boundary conditions are invariant under the combined effects of a shift in time \(T\) and a rotation by an angle \(fT\). If the turbulent statistics are expressed with respect to a similarly invariant reference frame, they will also be independent of phase angle once fully developed.
Numerical Details
The assumptions presented in this section are presumed to be valid only at high Reynolds numbers. The basic theory in this section is equivalent to Kazanski & Monin's (1961) or Casanady's (1967) work on the Ekman layer. Only the mean-velocity profiles and Reynolds stresses are considered, and the assumption is that the flow contains an inner and outer region, each with its own scaling, and that the inner and outer laws agree to leading order in an overlap region. For a full derivation and the notation used, please refer to Spalart (1989).
It was found that the basic theory is not in good agreement with the numerical results, although the situation improves with higher Reynolds numbers. In Spalart (1989) a higher order term is derived which had the potential of improving the agreement at low Reynolds numbers.
Available Results
The available data largely mirrors the profiles presented in Spalart (1989), and consists of
- Profiles of mean velocity and Reynolds stresses components
- Budgets of Reynolds stress components
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| File | Data available |
|---|---|
| 3d767-pt1.dat | Profiles of mean \(U\) and \(W\) velocity |
| 3d767-pt2.dat | Profiles of total and Reynolds shear stresses |
| 3d767-pt3.dat | Profiles of rms fluctuating velocities |
| 3d767-pt4.dat | Budget for \(2k\) |
| 3d767-pt5.dat | Budget for \(\overline{u^2}\) |
| 3d767-pt6.dat | Budget for \(\overline{v^2}\) |
| 3d767-pt7.dat | Budget for \(\overline{w^2}\) |
| 3d767-pt8.dat | Budget for \(\overline{uv}\) |
| 3d767-pt9.dat | Budget for \(\overline{vw}\) |
| 3d767-pt10.dat | Budget for \(\overline{uw}\) |
References
- Spalart, P.R. (1989). Theoretical and numerical study of a three dimensional turbulent boundary layer. J. Fluid Mech., Vol. 205, pp. 319-340.
- Coles, D.E. (1962). The turbulent boundary layer in an incompressible fluid. Appendix A: A manual of experimental practice for low-speed flow. pp. 35-74. Rand. Rep. R403-PR, ARC 24473.
- Kazanski, A.B., Monin, A.S. (1961). On the dynamical interaction between the atmosphere and the earth's surface. Bull. Acad. Sci. USSR, Ser. Geophys., Vol. 5, pp. 514-515.
- Casanady, G.T. (1967). On the resistance law of a turbulent Ekman layer. J. Atmos. Sci., Vol. 24, pp. 467-471.
Indexed data:
| case028 (dbcase, semi_confined_flow) | |
|---|---|
| case | 028 |
| title | Pseudo-Ekman Boundary Layer |
| author | Spalart |
| year | 1989 |
| type | DNS |
| flow_tag | 3d, 3dbl |