Time-Periodic Boundary Layer
Experiments by Jensen, Sumer, Fredsoe
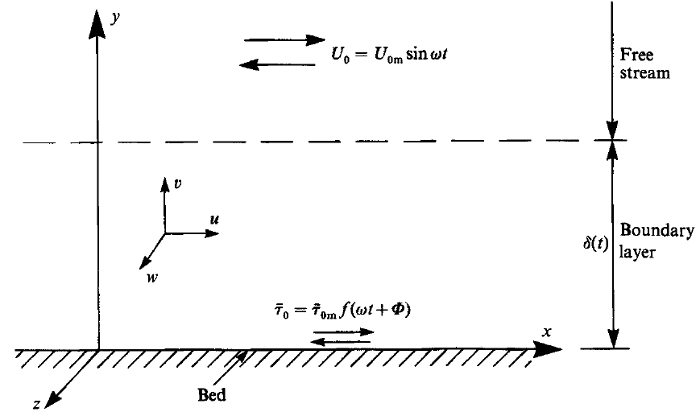
Description
The data is for turbulent oscillatory boundary-layer flow over a smooth wall. The free-stream flow is a purely oscillating flow with sinusoidal velocity variation. Mean and turbulence properties were measured mainly in two directions, namely in the streamwise direction and in the direction perpendicular to the wall. Some measurements were made also in the transverse direction. The measurements were carried out up to \(Re = aU_{om}/\nu = 6\times 10^6\) over a mirror-shine smooth bed, where \(U_{om}\) is the maximum of the free-stream velocity and \(a\) the amplitude of the free-stream oscillation, \(U_{om}/\omega\).
In Jensen et al (1989) the effect of changing \(Re\) and of introducing roughness elements onto the wall are also discussed and presented.
Experimental Details
Experimental Set-up
The experiments were carried out in a U-shaped oscillatory-flow water tunnel. The working section was 10 m long and 0.39 m wide. Its height was \(H = 0.28\) m in most of the tests of the present study. The top and side walls of the working section were made of smooth, transparent Perspex plates. The oscillatory flow in the tunnel was driven by an electronically controlled pneumatic system. In the tests, the flow was maintained near its resonant period, which is 9.72 s. The spectra of the velocity at the centreline of the tunnel indicated that the contributions from the second and third harmonics to the motion are negligible for all practical purposes.
The velocity distribution in the boundary layer over the bottom wall of the tunnel was measured for three different beds. These consisted of a smooth bed and two rough beds. For the smooth-bed tests PVC plates were fixed rigidly to the bottom of the tunnel. One of the rough beds of the tests was achieved by gluing a sheet of sandpaper on the bed. The roughness height of the sand paper was measured to be \(k = 0.35\) mm, and the density of the protrusions was 80 grains/cm2. This resulted in a Nikuradse's equivalent sand-roughness value of \(k_s = 0.84\) mm. The other rough bed, was obtained directly by gluing sand of fairly uniform size one layer deep to the actual bottom of the tunnel. The roughness height of this wall was measured to be \(k = 1.5\) mm. Its \(k_s\) value was found to be 2.6 mm for Test 14 and 3.7 mm for Test 15 (see table).
The velocities were measured by laser-Doppler anemometer (LDA). Two LDA systems were used in the measurements: a one-component system and a two- component system. The former was a Dantec LDA 04 System with a 15 mW H-Ne laser, which was used in forward-scatter mode. The system was equipped with a Dantec 55N10 frequency shifter and a Dantec 55N20 frequency tracker. The two-component system, on the other hand, was a Dantec two-colour high-performance fibre-optic LDA system with a Dantec 60\(\times\)11 fibre-optic probe head. A 100 mW argon laser was used in forward scatter mode with two Dantec 55N10 frequency shifters and two Dantec 55\(\times\)20 frequency trackers. To minimise the mismatch of the two pairs of laser beams in the two-component velocity measurements, the optic was rotated such that the planes formed by each pair of the beams were at 45o to the flow direction. The bed shear stress was measured with a Dantec 55R46 hot-film probe. These measurements were conducted only with the smooth bed. The probe was mounted flush to the bed in the middle of the working section. The one-component LDA system was used to monitor the free-stream velocity at the centreline of the tunnel simultaneously with the bed shear stress measurements. In order to ensure correct calibration, the shear-stress probe was calibrated in position.
Test Conditions
Table 1 summarises the test conditions for the measurements reported in Jensen et al (1989). The measurements available here correspond to Test number 10. \(U\), \(V\) and \(W\) are the flow velocities in the \(x\), \(y\) and \(z\) directions, respectively (see figure 1), \(U_{om}\) is the maximum value of the free-stream velocity defined by
\[ U_o = U_{om} \sin(\omega t) \]
\( \tau_o\) is the bed shear stress and \(U_{fm}\) is the maximum bed shear-stress velocity defined by
\[ U_{fm} = \left( \overline{\tau}_{om}/\rho\right)^{1/2} \]
where \(\rho\) is the fluid density and \(\overline{\tau}_{om}\) is the maximum value of the mean bed shear stress \(\overline{\tau}_{o}\):
\[ \overline{\tau}_o = \overline{\tau}_{om}f(\omega t + \phi) \]
where \(\phi\) is the phase lead of the maximum shear stress from the maximum value of the free-stream velocity \(U_{om}\), and \(f\) is a periodic function of time, generally dependent on Reynolds number and the bed roughness.
In the smooth-bed experiments reported here, \(U_{fm}\) was obtained by (i) direct measurements of the bed shear stress as described in the previous section and (ii) by fitting straight lines to the logarithmic-layer portion of the mean velocity distribution for those tests where the velocity distribution was measured. In the rough-bed experiments, on the other hand, \(U_{fm}\) was determined only by the latter method. This method gave also the Nikuradse's equivalent sand roughness \(k_s\). The values of \(k_s\) indicated in table 1 are those obtained in this way.
| \(U_{fm}\) (m/s) | ||||||||||||||
| Test no. | Period (s) | \(U_{om} (m/s)\) | \(a\) (m) | \(Re = aU_{om}/\nu\) | \(k\) (mm) | \(k_s\) (mm) | \(a/k_s\) | Direct meas. | From log fit | \(k_s^+ = k_sU_{fm}/\nu\) | Quantity measured | Apparatus | No. of cycles sampled | Sampling interval (ms) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Smooth wall | ||||||||||||||
| 1 | 9.72 | 0.073 | 0.113 | \(7.5 \times 10^3\) | - | - | - | 0.77 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 2 | 9.72 | 0.152 | 0.235 | \(3.3 \times 10^4\) | - | - | - | 1.1 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 3 | 9.72 | 0.23 | 0.36 | \(7.5 \times 10^4\) | - | - | - | 1.4 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 4 | 9.75 | 0.34 | 0.53 | \(1.6 \times 10^5\) | - | - | - | 1.7 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | |
| 5 | 9.72 | 0.45 | 0.70 | \(2.9 \times 10^5\) | - | - | - | 2.3 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 6 | 9.72 | 0.60 | 0.94 | \(5 \times 10^5\) | - | - | - | - | 3.2 | - | \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\), \(\left(\overline{v'^2}\right)^{1/2}\), \(\overline{u'v'}\) | Two-Comp. LDA | 80 | 24 |
| 7 | 9.72 | 0.68 | 1.05 | \(6.5 \times 10^5\) | - | - | - | 3.5 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 8 | 9.72 | 1.02 | 1.58 | \(1.6 \times 10^6\) | - | - | - | 4.8 | 4.9 | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 80 | 24 | |||||||||||
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\), \(\left(\overline{v'^2}\right)^{1/2}\), \(\overline{u'v'}\) | Two-Comp. LDA | 80 | 48 | |||||||||||
| 9 | 9.72 | 1.55 | 2.4 | \(3.4 \times 10^6\) | - | - | - | 6.4 | - | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| 10 | 9.72 | 2.0 | 3.1 | \(6 \times 10^6\) | - | - | - | 7.7 | 8.0 | - | \(\overline{\tau}_o\), \(\left(\overline{\overline{\tau}_o'^2}\right)^{1/2}\) | Hot film | 50 | 24 |
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 80 | 24 | |||||||||||
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\), \(\left(\overline{v'^2}\right)^{1/2}\), \(\overline{u'v'}\) | Two-Comp. LDA | 80 | 48 | |||||||||||
| 11 | 9.72 | 2.0 | 3.1 | \(6 \times 10^6\) | - | - | - | - | 8.0 | - | \(\left(\overline{\omega^2}\right)^{1/2}\) | Two-Comp. LDA | 80 | 48 |
| Rough wall with \(k = 0.35\) mm sand paper | ||||||||||||||
| 12 | 9.72 | 1.02 | 1.58 | \(1.6 \times 10^6\) | 0.35 | 0.84 | 1880 | - | 5.8 | 44 | \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 80 | 24 |
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\), \(\left(\overline{v'^2}\right)^{1/2}\), \(\overline{u'v'}\) | Two-Comp. LDA | 80 | 48 | |||||||||||
| 13 | 9.72 | 2.00 | 3.1 | \(6 \times 10^6\) | 0.35 | 0.84 | 3700 | - | 11.0 | 84 | \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 80 | 24 |
| \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\), \(\left(\overline{v'^2}\right)^{1/2}\), \(\overline{u'v'}\) | Two-Comp. LDA | 80 | 48 | |||||||||||
| Rough wall with \(k = 1.5\) mm sand grains | ||||||||||||||
| 14 | 8.12 | 0.87 | 1.13 | \( 9 \times 10^5\) | 1.5 | 2.6 | 435 | - | 6.0 | 142 | \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 50 | 14 |
| 15 | 8.12 | 2.1 | 2.71 | \( 5.2 \times 10^6\) | 1.5 | 3.7 | 730 | - | 14.0 | 460 | \(\overline{u}\), \(\left(\overline{u'^2}\right)^{1/2}\) | One-Comp. LDA | 50 | 14 |
Available Measurements
The data available are for Test number 10, at \(Re=6\times 10^6\). Data contained in the files consists of:
- Profiles across the boundary layer of mean velocity, rms velocities \(u'\), \(v'\), and turbulent shear stress \(\overline{uv}\) at phase angles from \(\theta=0^o\) to \(180^o\) in \(15^o\) steps.
- Mean and rms wall shear stress as functions of phase angle \(\theta\).
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| File | Data available |
|---|---|
| p10meanu.dat | Profiles of mean velocity \(U\) |
| p10rmsuu.dat | Profiles of rms velocity \(u'\) |
| p10rmsvv.dat | Profiles of rms velocity \(v'\) |
| p10reyuv.dat | Profiles of rms velocity \(\overline{uv}\) |
| p10tauw.dat | Mean wall shear stress vs \(\theta\) |
| p10trms.dat | Rms wall shear stress vs \(\theta\) |
The file readme.txt has additional information on the data files.
References
- Jensen, B.L., Sumer, B.M., Fredsoe, J. (1989). Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech., Vol. 206, p. 265.
Indexed data:
| case029 (dbcase, semi_confined_flow) | |
|---|---|
| case | 029 |
| title | Time-Periodic Boundary Layer |
| author | Jensen, Sumer, Fredsoe |
| year | 1989 |
| type | EXP |
| flow_tag | 2d, unsteady, 2dbl |