Backward-Facing Step
DNS by Le and Moin
Description
Simulation of flow over a backward-facing step.
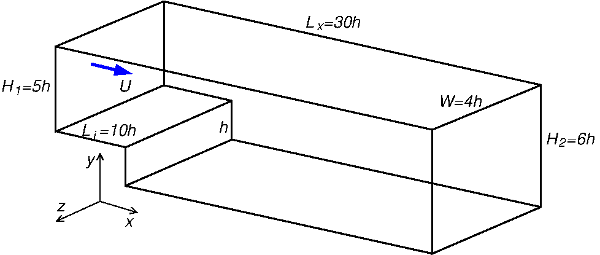
The mean velocity profile obtained from a boundary layer simulation by Spalart (1988) is imposed at the inlet at \(Re_{\theta}= 667\). Random velocity fluctuations \(u'\), \(v'\), and \(w'\) are superimposed on this profile according to a variant of the method of Lee et al. (1992). The fluctuations are prescribed such that, at the inlet, the turbulence intensities and Reynolds shear stress of Spalart's data are also duplicated. A convective boundary condition (Pauley et al., 1988) is imposed at the exit. The streamwise domain consists of an entry section of length \(10h\) prior to the step and a \(20h\) post-expansion section, where \(h\) is the step height. The vertical dimensions before and after the expansion are \(H_1 = 5h\) and \(H_2 = 6h\) which give an expansion ratio \(ER\) of 1.20 (see figure 1).
The Reynolds number, based on \(h\) and the mean inlet free stream velocity \(U_0\), is \(Re_h = 5100\).
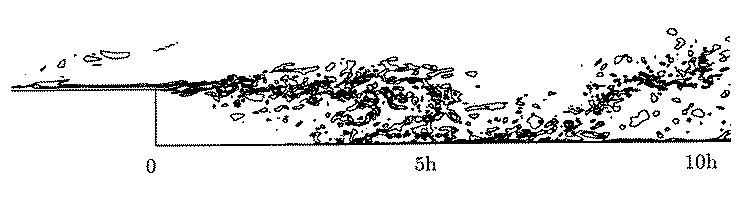 Fig. 2: Spanwise vorticity contours
Fig. 2: Spanwise vorticity contours
Contour plots of the instantaneous spanwise vorticity \(\omega_z\) on a typical vertical plane are shown in figure 2. The vorticity is normalised by \(U_0/h\). A free-shear layer spreading from the step and interacting with the lower wall near the mean reattachment location, \(x_R = 6h\), is discernible.
The basic statistical quantities are compared in Le et al (1997) to results from experiments by Jovic and Driver (1994), showing generally good agreement.
Simulation Details
The Navier-Stokes equations are discretized using a finite difference method on a staggered mesh. Uniform mesh spacing is applied in the streamwise (\(x\)) and spanwise (\(z\)) directions. In the vertical (\(y\)) direction, non-uniform mesh is employed with mesh refinement at the wall and near the step. The fractional step method from Le and Moin (1991) is used for time advancement. The Navier-Stokes equations are first advanced using a second-order semi-implicit method without the pressure terms. The pressure is then calculated by solving the Poisson equation, and the velocities are then corrected to satisfy the continuity equation.
The spanwise dimension, \(W\), is \(4h\) where periodic boundary conditions are imposed. The simulation uses \(770 \times 194 \times 66\) grid points in the streamwise, wall normal, and spanwise directions, respectively.
The computation used 13 megawords of memory and required approximately 55 CPU seconds per time step on a single processor CRAY Y-MP at a rate of 186 mflops. Statistical quantities are averaged over the spanwise direction and time. About 1100 CPU hours were required to obtain an adequate statistical sample. The total computational time corresponds to approximately 4.5 flow-through times.
Available results
Data available includes:
- Profiles of mean velocity and Reynolds stresses at \(x/h=-3\), \(4\), \(6\), \(10\), \(15\) and \(19\)
- Reynolds stresses budgets at \(x/h=-3\), \(4\), \(6\), \(10\), \(15\) and \(19\)
- Skin friction and boundary layer information at \(x/h=-3\), \(4\), \(6\), \(10\), \(15\) and \(19\)
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Location | Mean velocity and Reynolds stress profiles | \(\overline{u^2}\) Budget | \(\overline{v^2}\) Budget | \(\overline{w^2}\) Budget | \(\overline{uv}\) Budget | \(k\) Budget |
|---|---|---|---|---|---|---|
| \(x/h=-3\) | x-181.dat | rs11-181.dat | rs22-181.dat | rs33-181.dat | rs12-181.dat | rskk-181.dat |
| \(x/h= 4\) | x-360.dat | rs11-360.dat | rs22-360.dat | rs33-360.dat | rs12-360.dat | rskk-360.dat |
| \(x/h= 6\) | x-411.dat | rs11-411.dat | rs22-411.dat | rs33-411.dat | rs12-411.dat | rskk-411.dat |
| \(x/h=10\) | x-513.dat | rs11-513.dat | rs22-513.dat | rs33-513.dat | rs12-513.dat | rskk-513.dat |
| \(x/h=15\) | x-641.dat | rs11-641.dat | rs22-641.dat | rs33-641.dat | rs12-641.dat | rskk-641.dat |
| \(x/h=19\) | x-744.dat | rs11-744.dat | rs22-744.dat | rs33-744.dat | rs12-744.dat | rskk-744.dat |
Skin friction and boundary layer data are available in the file stat-inf.dat. The file readme.txt contains further information on the files.
References
- Jovic, S., Driver, D.M. (1994). Backward-facing step measurement at low Reynolds number, \(Re_h=5000\). NASA Tech. Mem. 108807.
- Le, H., Moin, P. (1991). An improvement of fractional step methods for the incompressible Navier-Stokes equations. J. Comput. Phys., Vol. 92, pp. 369-379.
- Le, H., Moin, P. (1992). Direct numerical simulation of turbulent flow over a backward-facing step. Stanford Univ., Center for Turbulence Research, Annual Research Briefs, pp. 161-173.
- Le, H., Moin, P., Kim, J. (1997). Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech., Vol. 330, pp. 349-374.
- Lee, S., Lele, S.K., Moin, P. (1992). Simulation of spatially evolving turbulence and the applicability of Taylor's hypothesis in compressible flow. Phys. Fluids A, Vol. 4, pp. 1521-1530.
- Pauley, L.L., Moin, P., Reynolds, W.C. (1988). A numerical study of unsteady laminar boundary layer separation. Report TF-34, Thermosciences Division, Dept. of Mech. Engng., Stanford University.
- Spalart, P.R. (1988). Direct simulation of a turbulent boundary layer up to \(R_{\theta}=1410\). J. Fluid Mech., Vol. 187, pp. 61-98.
Indexed data:
| case031 (dbcase, confined_flow) | |
|---|---|
| case | 031 |
| title | Backward-Facing Step |
| author | Le, Moin |
| year | 1992 |
| type | DNS |
| flow_tag | 2d, separated, varying_cross_section |