Channel Flow
DNS by Kim, Moin, Moser
Description
Direct numerical simulation of a turbulent channel flow where all essential scales of motion are resolved.
Two cases are reported, one with \(Re \approx 3300\) based on channel half height and centreline velocity, and the other with \(Re \approx 7890\). Corresponding Reynolds numbers based on wall friction velocity are \(Re_{\tau} = 180\) and \(395\).
Geometry
A diagram of the flow geometry and co-ordinate system are shown in figure 1. The channel half-width is denoted by \(\delta\).
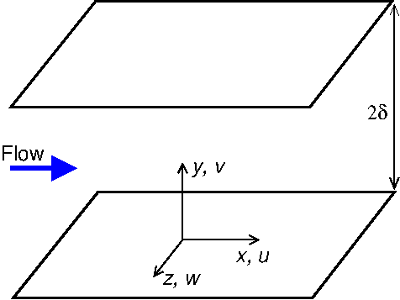 Fig. 1: Flow geometry and configuration
Fig. 1: Flow geometry and configuration
The initial choice of the computational domain was made by examining experimental two-point correlations. The computational domain was then adjusted as necessary to ensure that the turbulent fluctuations were uncorrelated at a separation of one half-period in the homogenous directions.
The computation was carried out with 3,962,880 grid points (\(192\times 129\times 160\), in \(x\), \(y\), \(z\) directions). For the Reynolds number \(Re_{\tau}=180\) the streamwise and spanwise computational periods were chosen to be \(4\pi \delta\) and \(2\pi \delta\) respectively (2300 and 1150 in wall units). With this computational domain, the grid spacings in the streamwise and spanwise directions were respectively \(\Delta x^+ \approx 12\) and \(\Delta z^+ \approx 7\) in wall units. Non-uniform meshes were used in the wall-normal direction with \(y_j = \cos(\theta_j)\) for \(\theta_j = (j-1)\pi/(N-1)\) for \(j = 1,2,....N\), where \(N\) is the number of grid points in the \(y\) direction. The first mesh point away from the wall was at \(y^+ \approx 0.05\) and the maximum spacing (at the centreline of the channel) was 4.4 wall units. No subgrid-scale model was used in the computation.
Flow Conditions/Parameters
Fully developed channel flow.
Computations carried out for Reynolds numbers of 3300 and 7890, based on the mean centreline velocity \(U_c\) and the channel half-width \(\delta\) (corresponding Reynolds numbers of 180 and 395 based on the wall shear velocity \(u_{\tau}\).
Simulation Details
Numerical Techniques
The governing equations for an incompressible flow can be written in the following form
\[ \frac{\partial u_i}{\partial t} = - \frac{\partial p}{\partial x_i} + H_i + \frac{1}{Re}\frac{\partial^2 u_i}{\partial x_j^2} \] \[ \frac{\partial u_i}{\partial x_i} = 0 \]
Here, all variables are non-dimensionalised by the channel half width \(\delta\) and the wall shear velocity \(u_{\tau}\). \(H_i\) includes the convective terms and the mean pressure gradient, and \(Re\) denotes the Reynolds number defined as \(Re = u_{\tau}\delta/\nu\).
These two equations are then solved to find the normal velocity and vorticity, the streamwise velocity \(u\), the spanwise velocity and pressure. For a full solution to these equations, please refer to Kim et al (1987).
The nonlinear terms in the momentum equations are computed in the rotational form (see Moin & Kim, 1982) to preserve the conservation property of mass, energy, and circulation numerically. In addition, the number of collocation points is expanded by a factor of 3/2 before transforming into the physical space to avoid the aliasing errors involved in computing the nonlinear terms pseudo-spectrally.
The accuracy of the numerical code was examined by computing the evolution of small-amplitude oblique waves in a channel. Both decaying (stable) and growing (unstable) waves were tested for \(Re_c = 7500\), based on the centreline velocity and the channel half width. These initial conditions were obtained from numerical solutions of the Orr-Somerfeld equations (Leonard & Wray, 1982). With 65 Chebychev polynomials, both decay and growth rates were predicted to within \(10^{-4}\)% of the value predicted by the linear theory when the initial energy either decreased or increased by a factor of 10%.
Computational Errors
The computed results are compared with experimental data at comparably low Reynolds numbers (Kreplin & Eckelmann, 1979). Although the general characteristics of the computed turbulence statistics are in good agreement with the experimental results, detailed comparisons in the wall region reveals consistent discrepancies. In particular, the computed Reynolds stresses - both the normal and shear stresses - are consistently lower than the measured values, while the computed vorticity fluctuations at the wall are higher than the experimental values.
One source of the discrepancy might be related to the measurement of the wall-shear velocity \(u_{\tau}\). When the mean-velocity profiles are renormalized with the corrected (experimental) \(u_{\tau}\), excellent agreement between the experimental results and the computed results is obtained. When the turbulence intensities and the Reynolds shear stress are similarly rescaled, the overall agreement is better, but the computed turbulence intensities, except the streamwise fluctuations, remain lower than the measured values. The use of hot-film probes to measure turbulence quantities in the proximity of the wall is another possible source of error.
Another source of the discrepancy may be the test section of the oil channel used in the experiments of Kreplin & Eckelmann (1979). The test section is 22 cm wide and 7m long and filled with oil to a depth of 85cm, which gives an aspect ratio of 3.9 (depth to width), and the length of the test section is 32 channel widths. This aspect ratio is well below the recommended minimum value of 7 to be representative of two-dimensional flow.
The disagreement between the computed and measured values are mostly confined to the immediate vicinity of the wall and do not seem to be serious.
Available Results
Data available consists of
- Profiles across the channel of mean velocity, Reynolds stresses, and triple moments
- Budgets of Reynolds stresses and turbulent kinetic energy
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Case | Profiles and stress budgets |
|---|---|
| \(Re_{\tau}=180\) | simul1.dat |
| \(Re_{\tau}=395\) | simul2.dat |
The data for both cases is also available in an Excel spreadsheet as all_results.xls.
References
- Kim, J., Moin, P., Moser, R. (1987). Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech., Vol. 177, pp. 133-166.
- Mansour, N.N., Kim, J., Moin, P. (1988). Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech., Vol. 194, pp. 15-44.
- Moin, P., Kim, J. (1982). Numerical investigation of turbulent channel flow. J. Fluid Mech., Vol. 118, pp. 341-377.
- Leonard, A., Wray A.A. (1982). A numerical method for the simulation of three-dimensional flow in a pipe. Proc. 8th Intl. Conf. On Numerical Methods in Fluid Dynamics, Aachen, Germany.
- Kreplin, H., Eckelmann, H. (1979). Behaviour of the three fluctuating velocity components in the wall region of a turbulent channel flow. Phys. Fluids, Vol. 22, p. 1233-1239.
Indexed data:
| case032 (dbcase, confined_flow) | |
|---|---|
| case | 032 |
| title | Channel Flow |
| author | Kim, Moin, Moser |
| year | 1987 |
| type | DNS |
| flow_tag | constant_cross_section, channel_flow |