Circular Air Jet
Experiments by Anselmet and Fulachier
Description
The aim of these experiments is to investigate the development of turbulent axisymmetric jets in the near field region, close to the nozzle exit. A vertical axisymmetric turbulent jet emitted from a fully developed pipe flow, weakly confined in coflowing air, is investigated. Special attention is paid to the near-field region, \(x/D_j \le 20\) where there is a lack of experimental results.
The data available here correspond to the equal density case (air jet into coflowing air). Two corresponding situations are also reported in Amielh et al (1996) with density ratio varying from 0.14 (He/air) to 1.5 (CO2/air), with the momentum flux \(Mj\) maintained constant.
Geometry
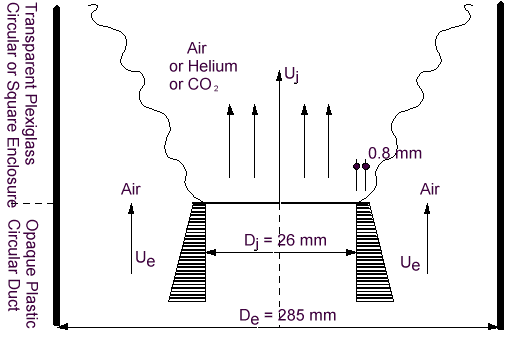
The experimental set-up used can be seen in the figure 1. The fully developed, turbulent, axisymmetric, vertical, ascending tube jet is emitted from a nozzle diameter \(D_j= 26\) mm, thickness 0.8 mm.
The coflowing air jet of external diameter \(D_e\), and velocity \(U_e \approx 1\) m/s, is provided by an opaque plastic circular duct which extends to a point level with the nozzle exit. The transparent confinement above this is provided by a square based test duct, 1.2m high, with a cross section of \(285 \times 285\) mm. This allows measurements at stations up to 40 times the diameter of the nozzle exit. Turbulence in the boundary layers, outside the primary tube and inside the secondary tube, is activated by 2mm thick areas of roughness elements located at approximately \(110 D_j\) upstream of the ejection section.
Measurement Techniques
Laser-Doppler velocimetry
The velocity field was determined by laser-Doppler velocimetry. The measurements were taken with a laser-Doppler system with two components, using the 488 and 514nm wavelength emission lines of a 4W Spectraphysics Argon source. The light is transmitted by an optical fibre, 10m long, from the source to the emission-reception head. Three beams, blue, green and common are emitted by the optic head via a converging lens with a focal length of 310mm. The measurement volume (\(0.12 \times 0.12 \times 1.32\) mm3) includes two systems of interfringes that are at right angles to each other. In order to obtain an equivalent sensitivity for the two signals, the interfringe planes are inclined at 45o in relation to the axis of the jet.
Silicon 710 oil was used as a marker, with density 1.11 and kinematic viscosity of 500mm2/s. The seeder was a SIBE diffuser, supplying particles of average diameter 1 \(\mu\)m that have a response time of a few micro-seconds and are therefore assumed to correctly follow the studied flow. The signal is processed with two DANTEC 57N10 Doppler burst spectrum analyzers.
Chemical analyzer
For the Helium and CO2 jet cases reported in Amielh et al (1996) measurements of the scalar field of mean mass fraction were taken using a SETNAG and LIEN ATK20 chemical analyzer. This apparatus gives the oxygen content of a mixture in the form of a voltage proportional to the percentage volume of oxygen.
Continuous samples of gas are put in contact with the sensitive element composed of a zirconia micro-gauge. From the electric potential generated, (and hence a voltage) the mean fraction of oxygen in the analyzed gas sample is deduced. This is then used to deduce the volumetric fraction \(X_{gas}\) of the considered gas in the analyzed sample. In this way, the mean fraction of the gas in the mixture, \(C\), can be calculated from the molecular masses \(M_{air}\) and \(M_{gas}\).
Data reduction
A convergence study of the calculations of the different moments of the velocity field was performed to optimize the number of points to be acquired in order to obtain moments in an acceptable manner, particularly for the helium jet. The study showed that a minimum of 12,000 validated points must be considered in order to obtain reasonable convergence for the moments, therefore measurements were performed by taking into account approximately 15,000 points for each of the two channels after coincidence.
Flow Characteristics
The flow emitted is a fully developed, turbulent, axisymmetric, vertical ascending jet.
By adopting an air coflow that produces a slightly round jet (\(D_e/D_j > 10\)), the boundary conditions for the purposes of modelling can be controlled. Among other things, the coflow resolves the problems of seeding found at the edges of the jet, thus providing good conditions for proper velocity measurements using laser-Doppler velocimetry. This secondary flow must remain sufficiently weak to avoid any radical change in the development of the jet, but must be of sufficient velocity to prevent recirculation zones from occurring. This problem is normally avoided when the Craya-Curtet parameter for variable density flows is maintained above 0.8, irrespective of the gas considered.
The overall character of the variable density jet cases is mainly governed by the Froude number expressing the ratio of the forces of inertia and gravity present at the jet emission. Three main regions of the jet can therefore be defined:
The first region is pure jet behaviour, including the potential core area, where forces of inertia predominate. In the case of an axisymmetric jet, according to Chen and Rodi (1980), it extends as far as the dimensionless abscissa \(X_I\) defined as
\[ X_I = (X_I/D_j)Fr_j^{-1/2} (\rho_j/\rho_e)^{-1/4} \approx 0.5 \]
where the initial Froude number is given by:
\[ Fr_j = \frac{\rho_j U_j^2}{| \rho_j - \rho_e| g D_j} \]
The second region is of plume behaviour, where the effects of gravity are preponderant and which starts at \(X_{II} \approx 10X_I\).
The third region is an intermediate region where the two types of forces coexist and the jet is called a “forced plume” jet.
The results reported in Amielh et al (1996) fall mainly into the first and intermediate regions.
Inflow Conditions
This study is mainly concerned with the region of “pure jet behaviour” and part of the region where the effects of gravity begin to show (\(x/D_j = 7.5\) and \(20\) respectively for helium and CO2). The momentum flux at the jet exit, \(M_j\), was therefore chosen as the constant control parameter and is defined as follows:
\[ M_j = 2 \pi \int_0^{\infty} \rho U^2 r\,dr = \frac{\pi \rho_j U_j^2 D_j^2}{4} \]
Given a fluid of density \(\rho_j\) and a nozzle diameter \(D_j\), the value of the flux \(M_j\) is controlled by the initial velocity of the fluid \(U_j\). Since the velocity of the coflow \(U_e\) is maintained constant for the three gases used, the adopted nominal operating conditions are summarized by a constant ratio \(M_j/M_e\) and are shown in the table below, along with the other nominal experimental conditions.
| Gas | \(U_j\) (m/s) | \(\rho_j/\rho_e\) | \(Re_j\) | \(Fr_j\) | Craya-Curtet parameter, \(Ct\) |
|---|---|---|---|---|---|
| Air | 12 | 1 | 21000 | – | 1.22 |
| Helium | 32 | 0.14 | 7000 | 643 | 1.29 |
| CO2 | 10 | 1.5 | 32000 | 1363 | 1.15 |
The Reynolds number of the flow must be sufficiently high so that it is turbulent at the exit.
For a velocity \(U_e > 0.75\) m/s, the turbulence generated by the roughness areas \(110 D_j\) upstream of the ejection ensures that the boundary layers between the two tubes join together before the experiment duct, thus providing a fully developed secondary flow.
Available Measurements
The data available corresponds to the air/air jet configuration and consists of
- Profiles of mean velocity, 2nd moments, skewness and flatness along the jet centreline.
- Profiles of mean velocity, 2nd moments, skewness and flatness across the jet at a number of streamwise locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Profile Location | Data | |
|---|---|---|
| \(U\), \(u'\), \(V\), \(v'\), \(\overline{uv}\), \(u\) & \(v\) skewness & flatness | \(U\), \(u'\), \(W\), \(w'\), \(\overline{uw}\), \(u\) & \(w\) skewness & flatness | |
| Jet centreline | caxa.dat | laxa.dat |
| \(x/D_j=0.2\) | ca0.dat | la0.dat |
| \(x/D_j=1\) | ca1.dat | |
| \(x/D_j=2\) | ca2.dat | la2.dat |
| \(x/D_j=3\) | ca3.dat | |
| \(x/D_j=4\) | ca4.dat | la4.dat |
| \(x/D_j=5\) | ca5.dat | |
| \(x/D_j=8\) | ca8.dat | la8.dat |
| \(x/D_j=10\) | la10.dat | |
| \(x/D_j=12\) | ca12.dat | la12.dat |
| \(x/D_j=14\) | la14.dat | |
| \(x/D_j=15\) | ca15.dat | |
| \(x/D_j=16\) | la16.dat | |
| \(x/D_j=20\) | ca20.dat | la20.dat |
| \(x/D_j=28\) | la28.dat | |
| \(x/D_j=30\) | la30.dat | |
References
- Amielh, M., Djeridane, T., Anselmet, F., Fulachier, L. (1996). Velocity near-field of variable density turbulent jets. Int. J. Heat Mass Transfer, Vol. 39, pp. 2149-2164.
- Chen, C.J., Rodi, W. (1980). Vertical Turbulent Buoyant Jets: A Review of Experimental Data. HMT Series 4. Pergamon Press, Oxford.
- Djeridane, T., Amielh, M., Anselmet, F., Fulachier, L. (1993). Experimental investigation of the near-field region of variable density turbulent jets. Proc. 5th Int. Symp. on Refined Flow Modelling and Turbulence Measurement, Paris.
- Ruffin, E., Schiestel, R., Anselmet, F., Fulachier, L. (1993). Second order modelling of variable density turbulent jets: evaluation in the near field region. Proc. 5th Int. Symp. on Refined Flow Modelling and Turbulence Measurement, Paris.
Indexed data:
| case038 (dbcase, free_flow) | |
|---|---|
| case | 038 |
| title | Circular air jet |
| author | Anselmet, Fulachier |
| year | 1993 |
| type | EXP |
| flow_tag | axisymmetric, jet |