Rotating Homogeneous Turbulence in Axisymmetric Contraction
Experiment by Leuchter and Dupeuble
Description
This investigation was carried out by the authors to investigate the effects of rotation on homogeneous anisotropic turbulence by superimposing solid-body rotation on axisymmetric contraction.
The investigation is restricted to the axial region of the flow where the rotation-induced non-uniformities of the velocity gradients are at a minimum, thereby providing satisfactory conditions of homogeneity for the turbulence.
Rotation superimposed on the contraction reduces the anisotropy of the Reynolds stresses produced by the contraction. This is because the rotation amplifies the rapid pressure-strain correlations.
This linear mechanism is confirmed by numerical results obtained in the framework of Rapid Distortion Theory.
Geometry
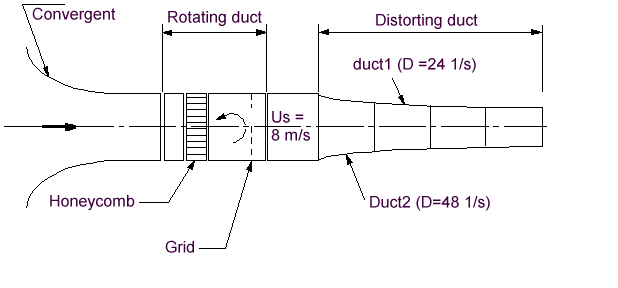
The test facility used for this experiment can be seen in figure 1.
The test facility produces solid body rotation by driving the flow through a rotating duct, 0.3 m in diameter, equipped with a fine-mesh honeycomb and a grid turbulence generator with an adjustable mesh size. The rotation rate (\(\Omega_o\)) can be adjusted.
The flow then enters a contracting duct designed to provide a constant strain rate \(D\) in the limiting case of zero rotation. The axial velocity under these conditions varies linearly between its initial value \(U_o\) and its final value \(U_1 = CU_o\), where \(C\) is the contraction ratio. The geometry of the duct is defined by:
\[ R(\xi) = R_o/(1+\beta\xi)^{1/2} \]
where: \(R(\xi)\) is the radius of the duct at the non-dimensional position \(\xi = x/L\) and \(R_o = R(0)\), \(L\) is the length of the duct, and \(\beta = DL/U_o\) is the dimensionless strain rate related to the contraction ratio by \(\beta = C - 1\).
In this experiment, the authors held the contraction ratio, \(C\), at a fixed value of 4.
All the experiments were run with the same inital velocity, thus the strain rate becomes inversely proportional to the length of the contracting duct.
Two different ducts were used during the experiment; duct 1, length 1m, yielding a strain rate of \(D=24\) s-1; and duct 2, length 0.5m, yielding a strain rate of \(D=48\) s-1. The maximum initial rotation rate is fixed at \(\Omega_o=48\) s-1, yielding a maximum rotation number \(\omega_o=\Omega_o/D=2\) for duct 1 and \(\omega_o =1\) for duct 2, For each duct two different experiments were made, one for \(\omega_o=0\) (reference case of pure contraction), the second for \(\omega_o = \omega_{o,max}\) (maximum rotation effects), as detailed in the table summarizing experimental conditions below.
| Duct | \(L\) [m] | \(D\) [1/s] | \(\Omega_{o,max}\) [1/s] | \(\omega_{o,max}\) |
|---|---|---|---|---|
| Duct 1 | 1 | 24 | 48 | 2 |
| Duct 2 | 1 | 48 | 48 | 1 |
Measurement Techniques
Mean flow and turbulence measurements are performed using conventional hot-wire techniques with crossed-wire probes.
The statistical quantities are determined through digital data processing from 204,800 simultaneous samples of both velocity components.
Integral length scales are evaluated from frequency spectra using the Taylor hypothesis.
Flow Characteristics
The effects of rotation on homogeneous anisotropic turbulence have been investigated with flow distortions produced by superimposing solid-body rotation on axisymmetric contraction. As shown by Batchelor (1967), this type of rotation-strain coupling generates non-uniformities in the mean flow gradients that are not present in planar distortions. In the central part of the flow, however, satisfactory conditions can be established for achieving transverse homogeneity in the turbulent field. The mean flow measurements confirming the theoretical predictions of Batchelor reveal that the turbulence actually is transversely homogeneous in the central part of the flow.
In the basic configuration of pure contraction, the distortion sharply impacts the anisotropy of the Reynolds stresses and the associated length scales (with the streamwise stress ratio, \(\overline{u^2}/k\), being reduced and \(\overline{v^2}/k\) and \(\overline{w^2}/k\) increased), confirming existing experimental results for axisymmetric contraction (with variable strain rates). Among the most pertinent effects of superimposed rotation, the measurements revealed a significant reduction in the anisotropy of the Reynolds stresses, and a correlative enhancement in that of the length scales.
Numerical predictions performed in the frame of Rapid Distortion Theory qualitatively confirm the more important features observed experimentally, especially the intense reduction of anisotropy. This comes about as a typical linear process in which the rapid pressure-strain correlation plays a central role.
Inflow Conditions
All of the experiments were run with same initial velocity of \(U_o = 8\) m/s.
The initial conditions for the turbulent field are the following (average values for duct 1):
| Turbulent Energy | \(k = 0.15\) (m/s)2 |
|---|---|
| Dissipation Rate | \(\varepsilon = 7.2\) m2/s3 |
| Ratio of RMS Values | \(u'/v' = 1.15\) |
| Longitudinal Lengthscale | \(L_{11,1} = 6.6\) mm |
| Transverse Lengthscale | \(L_{22,1} = 2.7\) mm |
The anisotropy in the initial state is slightly attenuated by the rotation. For duct 2, the corresponding energy and dissipation rate levels were found to be somewhat higher, by 10% and 7% respectively.
Linear Spectral Approach
The problem of rotation-strain coupling can be examined via Rapid Distortion Theory and a spectral type approach, leading to the conclusion that under those conditions the effect of the initial rotation is wholly defined by the ratio \(\omega_o = \Omega_o/D\). For details of such approaches, see Cambon et al (1985) and Leuchter (1993).
Available Measurements
For the four cases studied, measurements available include:
- The local strain rate
- The local rotation rate
- The axial mean velocity component
- The axial and transverse Reynolds stresses, \(\overline{u^2}\) and \(\overline{v^2}\)
- The trace of the Reynolds stress tensor, \(2k\)
- The dissipation rate
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
A short document summarizing the case is available as test39.pdf.
| \(\omega_o = \Omega_o/D\) | |||
| 0 | 1 | 2 | |
| Duct 1 (\(L=1\) m) | l100d0.dat | l100d2.dat | |
| Duct 2 (\(L=0.5\) m) | l50d0.dat | l50d1.dat | |
References
- Batchelor, G.K. (1967). An Introduction to Fluid Dynamics, Cambridge.
- Cambon, C., Teissedre, C., Jeandel, D. (1985). Etude d'effets couplés de déformation et de rotation sur une turbulence homogène. J. Méc. Théor. Appl., Vol. 4, pp. 629-657.
- Leuchter, O. (1993). Effects of rotation dominant distortions on homogeneous turbulence. Proc. 5th Int. Symp. on Refined Flow Modelling and Turbulence Measurement, Paris.
- Leuchter, O., Dupeuble, A. (1993). Rotating Homogeneous Turbulence Subjected to Axisymmetric Contraction. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
Indexed data:
| case039 (dbcase, free_flow) | |
|---|---|
| case | 039 |
| title | Rotating Homogeneous Turbulence in Axisymmetric Contraction |
| author | Leuchter, Dupeuble |
| year | 1993 |
| type | EXP |
| flow_tag | homogeneous, rotation |