Vortex Shedding Past Square Cylinder
Experiment by Lyn and Rodi
Description
Ensemble-averaged statistics at constant phase of the turbulent near-wake flow (Reynolds number = 21400) around a square cylinder have been obtained from two-component laser-Doppler measurements.
The turbulent flow around a square cylinder (a definition sketch is given in figure 1) has received far less attention than the flow around a circular cylinder. The topology of both flow fields is expected to be identical, but differences in length and velocity scales provide insight into the relationship between 'coherent' vortex structures and 'incoherent' (or 'random') turbulence characteristics.
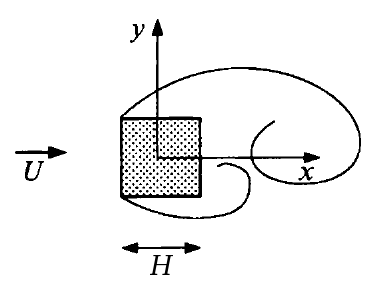 Fig. 1: Flow configuration and geometry
Fig. 1: Flow configuration and geometry
| Parameter | Present |
|---|---|
| \(Re\) | 21400 |
| Free-stream turbulence level (%) | 2 |
| Blockage (%) | 7 |
| Aspect ratio | 9.75 |
| Strouhal number | 0.13 |
| Measurement method | LDV |
| Measurement region | \(-0.5 \leq x/H \le 8\); \(0 \leq y/H \leq 2.5\) |
The present work reports on an LDV study, in which the mean, the periodic, and the random component of the flow around a square cylinder at a Reynolds number of 21400 were obtained from averaging at constant phase. With its directional sensitivity, the LDV was considered essential for reliable measurements in the highly turbulent base region with instantaneous flow reversals. As a single-point technique, however, a local phase reference could not be used, so a technique was adopted for defining a reference phase. Because only a limited number of phases were used, only the largest scales corresponding to the shedding and shed vortices were resolved. The 'random' component may be alternatively viewed as a residual, analogous to subgrid scales in large-eddy simulation.
Experimental Details
The experiments were performed in a closed water channel supplied by a constant- head tank. At the measurement station, the channel had a 39 cm by 56 cm cross-section (cf. the square cylinder's edge of length \(H = 4\) cm). The origin of the coordinate system used in the following is located in the centre of the cylinder, and all distances are non-dimensionalized by \(H\) (figure 1). A reference velocity, \(U\), was computed from time-averaged velocity profiles to be \(U = 0.535\) m/s. This is estimated to be within 2-3% of the average cross-sectional velocity. Unless otherwise specified, all velocity quantities are non-dimensionalized with \(U\). The Reynolds number, based on \(U\) and \(H\) was \(Re = 21400\). The shedding frequency, \(f\), was estimated as 1.77 +/-0.05 Hz from a direct analysis of the low-pass-filtered pressure signal with the peak-finding algorithm used in the phase-sorting procedure. This estimate agreed within experimental error with an estimate based on spectral analysis of the raw pressure signal. The resulting Strouhal number \(St = f H/U = 0.132 \pm 0.004\).
A two-colour LDV forward-scatter system measured two components of instantaneous point velocities. A reference phase was defined from a low-pass-filtered pressure signal taken from a tap at the midpoint of the cylinder sidewall. The time of occurrence of an LDV velocity realisation was marked in relation to the pressure signal, permitting the association of the velocity data with a particular phase of the vortex shedding cycle. All velocity realisations occurring within the same phase bin or interval constituted an ensemble at constant phase, so that statistics at constant phase could be evaluated.
A total of 20 phase bins was used, which, for a cycle period of 565 ms, implied a bin width of 28 ms. Because of slow data transfer and computer evaluation of the Doppler signal, the LDV signal processing system had a dead time of 100 ms, such that successive velocity realisations were necessarily placed in different phase bins and therefore different ensembles. As a result, the ensemble averages should be free of McLaughlin-Tiederman LDV bias.
The number of samples in a bin varied depending on measurement point location, with a maximum of 400 samples per phase bin in the region directly behind the cylinder. The duration of a measurement at a point was generally of the order of 1 hr (at some problem points such as in the recirculation region or at points where the optical quality of the glass window was inferior, it could be several hours), or, in terms of shedding cycles, of \(O(10^4)\) cycles.
Measurements were confined to the upper half of the flow region in order to reduce the number of measurements needed. It was assumed that the flow in the lower half could be obtained by reflecting the measured upper flow about the centreline. The streamwise measurement grid began at the leading edge of the cylinder and extended to \(x/H = 8\), and included an 'inlet' profile at \(x/H = -3\). In the lateral direction, the grid extended from the centreline to \(y/H = 2\) in the immediate vicinity of the cylinder, and to \(y/H = 2.5\) further downstream, as well as selected points on the streamwise grid at \(y/H = 4\). In the region \(x/H < 3\), \(y/H < 1.5\), the grid size was 0.125, but outside this region this was increased to 0.25 or more. Within 1 cm of the cylinder, optical access by the four-beam LDV system could not be maintained, so that two-component measurements were not performed in this region.
Measurement Errors
Several checks on consistency were made on the data to provide an indication of their quality, and are discussed in more detail in Lyn (1992). The integrated flow discharge from \(y/H = -4\) to \(y/H = 4\) remained constant in the wake region to within 2% for both the time-averaged and for each of the phase-averaged fields. At \(x/H = 8\), the time-averaged drag coefficient was estimated from the integral of the time-averaged streamwise momentum flux to be 2.1, which agrees with accepted literature values. For a symmetric time-averaged two-dimensional field, both \(\overline{V}\) and \(\overline{uv}\) should vanish on the centreline. The average over all measured centreline points for \(\overline{V}\) was -0.04, and for \(\overline{uv}\) was -0.007. These may be compared with maximum absolute values of \(\overline{V}\) and \(\overline{uv}\) which exceeded 0.3 and 0.1 respectively.
These comparisons give some support to the two-dimensionality achieved in the flow. The validity of the reflection procedure was examined by considering the centreline measurements of the ensemble-averaged fields, since the reflection procedure results in an additional measurement at each centreline point.
The average magnitude of the difference between the original and the reflected ensemble-averaged measurements on the centreline for \(\langle u\rangle\), \(\langle v\rangle\) and \(\langle -u'v'\rangle\) was typically 0.01, 0.07, and 0.006. From these checks, the uncertainty in the ensemble-averaged results for \(\langle u\rangle\), \(\langle v\rangle\), \(\langle u'\rangle\), \(\langle v'\rangle\) is estimated to be less than 0.05, with the largest uncertainty in \(\langle v\rangle\). In terms of the profile maximum, the uncertainty in \(\langle -u'v'\rangle\) is expected to lie in the range 15-25% in the region of large profile maxima, e.g. in the base region, but may be larger further downstream as the profile maxima in \(\langle -u'v'\rangle\) decrease. The uncertainty in quantities based on estimates of velocity gradients may be substantial. Estimates of local divergences \((\partial \langle u\rangle/\partial x + \partial \langle v\rangle/\partial y)\) could attain magnitudes of 1 or more at isolated points.
Available Measurements
Data available includes profiles of:
- Long-time-averaged mean velocity, Reynolds stresses and flatness factors at a number of streamwise (\(x\)) locations
- Phase-averaged mean velocity, Reynolds stresses and flatness factors at 20 phase positions through the vortex shedding cycle at the same \(x\) locations
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt contains some description of the data files.
Long-time-averaged data:
Phase averaged data 1, \(\phi=0^o\):
Phase averaged data 2, \(\phi=18^o\):
Phase averaged data 3, \(\phi=36^o\):
Phase averaged data 4, \(\phi=54^o\):
Phase averaged data 5, \(\phi=72^o\):
Phase averaged data 6, \(\phi=90^o\):
Phase averaged data 7, \(\phi=108^o\):
Phase averaged data 8, \(\phi=126^o\):
Phase averaged data 9, \(\phi=144^o\):
Phase averaged data 10, \(\phi=162^o\):
Phase averaged data 11, \(\phi=180^o\):
Phase averaged data 12, \(\phi=198^o\):
Phase averaged data 13, \(\phi=216^o\):
Phase averaged data 14, \(\phi=234^o\):
Phase averaged data 15, \(\phi=252^o\):
Phase averaged data 16, \(\phi=270^o\):
Phase averaged data 17, \(\phi=288^o\):
Phase averaged data 18, \(\phi=306^o\):
Phase averaged data 19, \(\phi=324^o\):
Phase averaged data 20, \(\phi=342^o\):
References
- Lyn, D.A. (1992). Ensemble-averaged measurements in the turbulent near wake of a square cylinder: a guide to the data. Rep. CE-HSE-92-6, School of Civil Engng., Purdue University.
- Lyn, D.A., Rodi, W. (1994). The flapping shear layer formed by flow separation from the forward corner of a square cylinder. J. Fluid Mech., Vol. 267, pp. 353-376.
- Lyn, D.A., Einav, S., Rodi, W., Park, J.H. (1995). A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech., Vol. 304, pp. 285-319.
- Murakami, S., Mochida, A. (1995). On turbulent vortex shedding flow past 2d square cylinder predicted by CFD. Journal of wind engineering and industrial aerodynamics, Vol. 54-55, pp. 192-211.
Indexed data:
| case043 (dbcase, flow_around_body) | |
|---|---|
| case | 043 |
| title | Vortex Shedding Past Square Cylinder |
| author | Lyn, Rodi |
| year | 1994 |
| type | EXP |
| flow_tag | 2d, unsteady, separated, bluff_body |