2D Channel Flow with/without Scalar Transport
DNS by Horiuti
Description
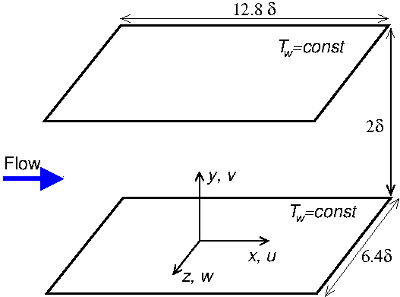
The flow field is a fully developed two-dimensional turbulent flow between two parallel flat plates as shown in figure 1. Passive scalar transport is calculated, with the scalar being uniformly input within the fluid and then removed at both walls. Wall temperatures (the scalar) at the two plates are set equal.
Flow conditions are:
- Reynolds number based on centreline velocity, \(Re_{\delta} = 3245\)
- Reynolds number based on friction velocity, \(Re_{\tau} = 180\)
- Molecular Prandtl number, \(Pr = 0.7\)
Simulation Details
The Navier-Stokes, continuity and passive scalar transport equations were discretized using Fourier series expansion in the \(x\) and \(z\) directions (128×128), and Chebyshev polynomial expansions in the \(y\) direction (128). Time-integration was done by combining the Second-order Adams-Bashforth scheme for nonlinear terms and the Crank-Nicolson scheme for the viscous and pressure-gradient terms. The continuity condition was enforced using the Kleiser-Schumann method combined with the Influence Matrix technique.
Size of computational domain: \(12.8\delta\) (\(x\) direction) by \(6.4\delta\) (\(z\) direction) by \(2\delta\) (\(y\) direction).
Grid spacing: 18 and 9 viscous units in the \(x\) and \(z\) directions, respectively.
Integration time for ensemble averaging of statistical values: Approximately \(5\delta/u_{\tau}\) after a fully developed state was reached.
Turbulence statistics for the dynamic field are normalized by \(u_{\tau}\) and \(\nu\), while scalar statistics are normalized by \(t_{\tau}\).
Available Results
Available data includes profiles across the channel of:
- Mean velocity and Reynolds stresses
- Skewness and flatness factors
- Turbulent kinetic energy and Reynolds stress budgets
- Mean scalar
- Turbulent scalar fluxes
- Scalar variance and its dissipation rate
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| File | Description |
|---|---|
| ch12_pg_wl3.dat | Dynamic field data |
| ch122_pg_wl3.dat | Scalar and dynamic field data |
References
- Horiuti, K. (1992). Assessment of two-equation models of turbulent passive-scalar diffusion in channel flow., J. Fluid Mech., Vol 238, pp. 405-433.
Indexed data:
| case044 (dbcase, confined_flow) | |
|---|---|
| case | 044 |
| title | 2D Channel Flow with/without Scalar Transport |
| author | Horiuti |
| year | 1992 |
| type | DNS |
| flow_tag | scalar, constant_cross_section, channel_flow |