Homogeneous Turbulent Shear Flows
Direct Numerical Simulation by Matsumoto, Nagano and Tsuji
Description
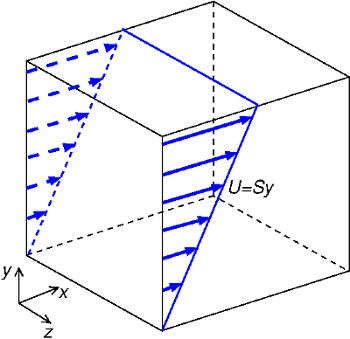
A sheared homogeneous turbulent field is simulated, as shown schematically in figure 1. The mean flow is imposed in the \(x\)-direction and is sheared in the \(y\)-direction at a constant shear rate \(S\). The initial non-dimensional shear rate \(Sk_o/\varepsilon_o\) is approximately 4.7. Turbulence statistics are obtained up to a dimensionless time \(St=14\). The flow does not have proper scales for non-dimensionalizing the governing equations, so that the computation is carried out in arbitrary units.
Numerical Method
The numerical method used for the present direct numerical simulation of homogeneous sheared turbulence is based on the spectral method developed by Rogallo (1981).
The time-dependent Navier Stokes and continuity equations are solved in a computational box of size \(2\pi \times 2\pi \times 2\pi\). The equations are discretized using spectral methods, with \(64\times 64\times 64\) Fourier modes in the \(x\), \(y\) and \(z\) directions, and a second order Runge-Kutta scheme for time integration. Remeshing is done at constant intervals, in order to advance the simulation in a coordinate system moving with mean flow (See Rogallo, 1981).
The velocity field is initialized to be an isotropic state in wave space, satisfying the continuity condition and the given energy spectrum, \(E(k)= 8.417\times 10^{-3}k^2\) for \(k \le 11\) and \(E(k)= 8.417\times 10^{-3}\times (11^{11/3})k^{-5/3}\) for \(11 \le k \le 30\).
Available Results
Data available include:
- Time development of Reynolds stresses
- RMS values of fluctuating velocities, strain rates and pressure
- Skewness and flatness factors
- Length- and time-scales
- Budget terms from the Reynolds stress equations
- One dimensional energy spectra
- Two point correlations
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as the single uncompressed file.
| Datafile | |
| Dynamic field data | sh12_ut_hm1.dat |
References
- Matsumoto, A., Nagano, Y., Tsuji, T. (1991). Direct numerical simulation of homogeneous turbulent shear flow. Proc. 5th Symposium on Computational Fluid Dynamics, Tokyo.
- Rogallo, R.S. (1981). Numerical Experiments in Homogeneous Turbulence, NASA TM 81315.
Indexed data:
| case049 (dbcase, free_flow) | |
|---|---|
| case | 049 |
| title | Homogeneous Turbulent Shear Flows |
| author | Matsumoto, Nagano, Tsuji |
| year | 1992 |
| type | DNS |
| flow_tag | homogeneous |