Boundary Layer in a S-Shaped Channel
Experiments by Truong and Brunet
Description
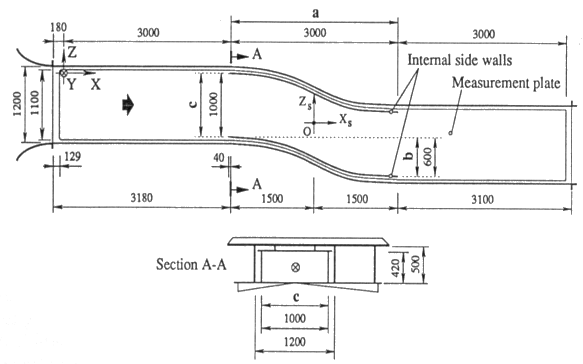
The experiment was conducted with the purpose of studying a pressure gradient driven three-dimensional boundary layer, to provide a comprehensive data base to examine critically different turbulence models. There are a number of ways to produce a three-dimensional boundary layer: e.g. by using appropriate curved walls to generate a transverse pressure gradient, by arranging for a local transverse motion of one bounding surface, by introducing a two-dimensional body mounted normal to a flat plate, etc… As the number of measurements to be carried out to define a three-dimensional flow development in satisfactory detail is large, due to the extra dimension involved, special attention must be paid to facilitate variations of different parameters governing the flow and to give easy access to different kinds of instrumentation. To achieve these goals, an S-shaped duct geometry was chosen, as shown in figure 1, to produce a series of experiments with gradual variation in crossflow inducing and relaxing features to improve the understanding of the physics of turbulence in three-dimensional boundary layer flows. In this type of duct, the flow is pressure-gradient driven and the ratio of shear forces to pressure forces can be varied at will; the S-shape geometry also exhibits the interesting feature of “cross-over” of the crossflow profile since the external streamlines in the core of the duct have an inflection point (Truong & Brunet, 1992).
Reynolds number \(Re_{\delta} = 110,000\).
Experimental Details
The tunnel, which is semi-closed and mounted vertically, has a test section consisting of three consecutive parts: a first straight part followed by a “S”-shaped part (the “S” is horizontal like a snake on a flat horizontal surface), which in turn is followed by a second straight part. Each part is 3 metres long, 0.5 metre high and 1.2 metre wide; in the S-part the width between the internal side walls is 1 metre. The flow enters the first straight portion with a nominally uniform velocity of 18 m/s at the exit section of the tunnel contraction with a contraction ratio of 7.35, the geometrical shape of which is chosen according to a cubic equation.
A free floating, polished, perfectly planar aluminium plate of thickness 6 millimetres with an elliptical leading edge facing the tunnel contraction exit, is mounted at 0.08 metre below and all along the roof of the tunnel test section. The plate is 1 metre wide with upwards curved lips of 50 millimetres wide at both sides on the first 3.5 metres from the leading edge. This measurement plate has 1000 static pressure tappings to determine the pressure distribution on the first 6 metres and 15 surface plugs interchangeable and flush mounted at defined stations for surface probes. The pressure lines are assembled between the roof of the tunnel and the measurement plate; great care was paid to keep at a minimum level the flow blockage effect. However, some blockage is still evident in the measurements.
The shape of the curved side walls in the “S” part of the duct is given by \[ z_s = -\frac{b}{2} \frac{\tanh(x_s/d)}{\tanh(a/(2d))} \pm \frac{c}{2} \] where the coordinates \(x_s\) and \(z_s\) are relative to the centre of the bend section, as shown in figure 1, and the constants \(a\), \(b\), \(c\) and \(d\) are given by (all having dimensions of metres): \(a=3\), \(b=0.6\), \(c=1\) and \(d=0.65\).
Measurement techniques
Velocities measured using X-wire probes and 3-wire probes. Skin friction measured with Preston tube.
Available measurements
Data available includes:
- Surface pressure measurements along the upstream and S-shaped duct wall
- Skin friction at 3 streamwise locations upstream of the S-shaped part
- Profiles of mean velocities and Reynolds stresses at a number of streamwise and spanwise locations upstream, and in the S-shaped duct section
Note that in the data files, coordinates \(X\), \(Y\), \(Z\) are used, with the origin at one upstream corner of the duct, as shown in figure 1. Values of \(Z\) are therefore negative throughout the duct.
Sample plots of selected quantities are available.
The data files can be downloaded as compressed archives from the links below, or as individual files from the tables.
| Freestream reference values | m01-op.dat |
| \(C_p\) measurements | m01-cp.dat |
| \(C_f\) measurements | m01-cf.dat |
| Profiles of Mean Velocity and Reynolds Stresses Upstream of the Bend Section | |||
|---|---|---|---|
| \(Z\) [mm] | \(X=1130\) mm | \(X=1195\) mm | \(X=1255\) mm |
| -0060 | x1130-z0060-vp.dat | x1195-z0060-vp.dat | x1255-z0060-vp.dat |
| -0250 | x1130-z0250-vp.dat | x1195-z0250-vp.dat | x1255-z0250-vp.dat |
| -0437 | x1130-z0437-vp.dat | x1195-z0437-vp.dat | x1255-z0437-vp.dat |
| -0500 | x1130-z0500-vp.dat | x1195-z0500-vp.dat | x1255-z0500-vp.dat |
| -0563 | x1130-z0563-vp.dat | x1195-z0563-vp.dat | x1255-z0563-vp.dat |
| -0750 | x1130-z0750-vp.dat | x1195-z0750-vp.dat | x1255-z0750-vp.dat |
| -0940 | x1130-z0940-vp.dat | x1195-z0940-vp.dat | x1255-z0940-vp.dat |
| Profiles of Mean Velocity and Reynolds Stresses in the Bend and Vicinity | ||||
|---|---|---|---|---|
| \(X\) [mm] | \(Z=-0340\) mm | \(Z=-0500\) mm | \(Z=-0660\) mm | |
| 2945 | x2945-z0340-vp.dat | x2945-z0500-vp.dat | x2945-z0660-vp.dat | |
| 3320 | x3320-z0340-vp.dat | x3320-z0500-vp.dat | x3320-z0660-vp.dat | |
| \(X\) [mm] | \(Z=-0646\) mm | \(Z=-0800\) mm | \(Z=-0960\) mm | |
| 4125 | x4125-z0646-vp.dat | x4125-z0800-vp.dat | x4125-z0960-vp.dat | |
| \(X\) [mm] | \(Z=-0730\) mm | \(Z=-0890\) mm | \(Z=-1050\) mm | \(Z=-1250\) mm |
| 4700 | x4700-z0730-vp.dat | x4700-z0890-vp.dat | x4700-z1050-vp.dat | x4700-z1250-vp.dat |
| \(X\) [mm] | \(Z=-0850\) mm | \(Z=-1000\) mm | \(Z=-1150\) mm | \(Z=-1300\) mm |
| 5005 | x5005-z0850-vp.dat | x5005-z1000-vp.dat | x5005-z1150-vp.dat | x5005-z1300-vp.dat |
| 5255 | x5255-z0850-vp.dat | x5255-z1000-vp.dat | x5255-z1150-vp.dat | x5255-z1300-vp.dat |
| \(X\) [mm] | \(Z=-1068\) mm | \(Z=-1198\) mm | \(Z=-1328\) mm | |
| 5500 | x5500-z1068-vp.dat | x5500-z1198-vp.dat | x5500-z1328-vp.dat | |
References
- Truong, T.V., Brunet, M. (1992). Test case T1: Boundary layer in a S-shaped channel. Numerical Simulation of Unsteady Flows and Transition Turbulence (Eds: O. Pinomeau, W. Rodi, I.L. Tyhming, A.M. Savill, T.V. Truong), Cambridge University Press.
Indexed data:
| case051 (dbcase, semi_confined_flow) | |
|---|---|
| case | 051 |
| title | Boundary layer in an S-shaped channel |
| author | Truong, Brunet |
| year | 1989 |
| type | EXP |
| flow_tag | 3d, curvature, 3dbl, constant_cross_section |