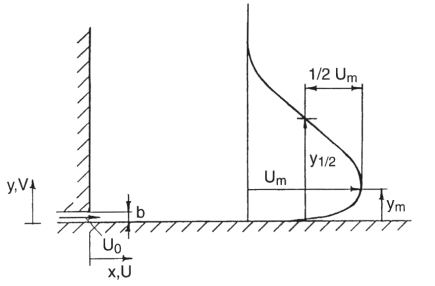
2D Plane Turbulent Wall Jet
Experiments by Karlsson, Eriksson, Persson
Description
Laser-Doppler measurements were conducted in a plane turbulent wall jet at a Reynolds number based on inlet velocity, \(Re_o\), of 9600. The initial development, as well as the fully developed flow, was studied. Special attention was given to the near-wall region, including the use of small measuring volumes and the application of specific near-wall data corrections, so that wall shear stresses were determined directly from the mean velocity gradient at the wall using only data below \(y^+ = 4\). It was possible to resolve the inner peak in the streamwise turbulence intensity as well as the inner (negative) peak in the shear stress.
Experimental Details
The basic flow field of interest here was the two-dimensional wall jet on a plane surface, and more specifically “the plane wall jet in still air” according to the terminology used by Launder & Rodi (1981). There are, however, variations on this subcategory of the wall jet. One of these variations concerns the design of the wall above the inlet. This wall is usually either a thin lip or an “infinite” vertical wall as in the present experiment (figure 1). The latter design is simpler to treat computationally, since it, together with a “no inflow” upper boundary, results in a single, well-defined inflow boundary with known boundary conditions. It was therefore chosen here, in spite of the inevitable return flow that this configuration generates, a return flow which far downstream of the nozzle does change the character of the jet.
An important criterion in the experimental design was that the spatial resolution should be sufficiently high to allow the wall shear stress to be determined directly from mean velocity measurements. This imposes an upper limit on the ratio of measuring control volume diameter to viscous length scale, but a high enough inlet Re-number must also be retained to allow comparisons with earlier studies. Once water was chosen as the working fluid, due to the absence of seeding problems in low-speed water flows, these considerations led to the present combination of slot width and inlet velocity.
Wall Jet Test Facility
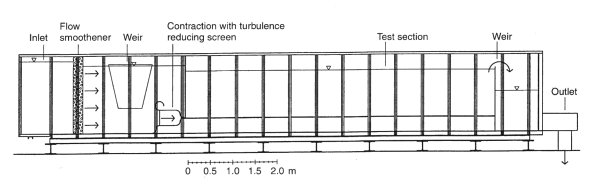 Fig. 2: Experimental test facility layout
Fig. 2: Experimental test facility layout
The test facility is shown in figure 2. It consists of a large tank into which a jet discharges. The tank is 7 m long and its width is 1.45 m. One of the side walls is made of glass, as well as the bottom. (Using a glass bottom improves the conditions for near-wall measurements, since its smoothness minimises the diffuse surface reflections (Johnson & Brown, 1990).) The slot height was measured with water in the tank, by a diver. The results showed the slot height to be 9.6 +/- 0.1 mm over most of the slot width. Given the uncertainties involved, this is consistent with an indirect determination of the slot height using the volumetric flow rate. Consequently, \(b = 9.6\) mm will be used in the following analysis, giving a jet width-to-height ratio of 151. This was considered large enough to obtain good two-dimensionality.
A large contraction (Morel, 1975) with a turbulence-reducing screen inserted is used to produce a fairly flat mean velocity profile at the inlet. A weir upstream of the contraction keeps the upstream water level constant, and the flow velocity through the slot is set by an adjustable weir at the downstream end at the tank. This reference velocity is determined as
\[ U_o = \sqrt{2g \Delta h} \]
where \(\Delta h\) is the difference in height between the upstream and downstream free surfaces. The inlet velocity, \(U_o\), was set as close as possible to 1 m/s, corresponding to a water depth downstream of the inlet of about 1.4 m. For this water depth, the influence of the re-circulating flow on the growth rate of the jet was negligible for the first 150 slot heights.
Using water of approximately room temperature, one obtains a nominal inlet Reynolds number:
\[ Re_o = \frac{U_ob}{\nu} \approx 9.6\times 10^3 \]
which is sufficiently high to be comparable to previous experimental studies, e.g. Bradshaw & Gee (1960) and Tailland & Mathieu (1967).
Instrumentation
The LDV hardware consisted of a modified TSI two-colour system. The system was modified to increase the beam expansion ratio to 8.5 by including an extra beam expansion module. An upper-central beam arrangement was used to measure the normal velocity component (\(V\)). A front lens with a focal distance of 750 mm was used, in order to reach the centreline of the tank. The measuring volume sizes were (\(0.73 \times 0.05\)) mm (streamwise velocity component, 488 nm) and (\(1.60 \times 0.05\)) mm (normal velocity component, 514.5 nm), respectively. Silicon carbide particles with a mean diameter of 1.5 \(\mu\)m were used to uniformly seed the flow.
With the exception of the positions closest to the wall, where only the streamwise velocity component was measured, all measurements were made in coincidence mode; requiring the bursts in channel 1 and channel 2 to arrive within a certain, pre-determined, time interval. Shift frequencies were chosen such that all likely flow angles were measured with equal probability (Whiffen, 1975; Buchhave, 1975, 1979), while still staying away from the filter limits.
Experimental Procedure and Flow Qualification
Outline of Measurements
Extensive Pitot-tube measurements, spanwise profiles at several heights and numerous vertical profiles at different spanwise positions, were made at the slot (\(x = 0\)) to check for symmetry and spanwise variations. Part of the inlet velocity profile was also measured using LDV, to resolve better the boundary layer and to get turbulence data. LDV measurements, streamwise and spanwise profiles, were also taken immediately downstream of the slot. Extensive spanwise measurements were made at several streamwise positions in order to check the two-dimensionality of the flow. Based on these spanwise measurements, it was decided to make the main measurement series approximately halfway between the centreline and the glass wall. The flow conditions in that spanwise position were identical to those at the centreline within the measurement accuracy. The main measurement series were taken at the following streamwise positions: \(x = 50\), \(100\), \(200\), \(400\), \(700\), \(1000\), \(1500\), \(2000\) mm. For the sake of simplicity, the text below refers to these positions as \(x/b = 5\), \(10\), \(20\), \(40\), \(70\), \(100\), \(200\), although the actual dimensionless distance was about 4% larger. Measurements stopped at \(x/b = 200\) because the flow was losing its wall-jet character by that distance.
Main Measurement Series
The vertical profiles of the main measurement series were taken in order, starting from \(x/b = 5\) and working downstream. \(\Delta h\) and the water temperature, \(T_o\), were checked regularly, in order to detect any drift in inlet velocity or inlet Re-number. There was essentially no change in \(U_o\) or \(Re_o\) during the individual profiles. There were, however, small variations between the different profiles due to a 3% variation in the boundary conditions, i.e. \(Re_o\). Where relevant, all velocities have been normalised to the same inlet velocity by multiplying with \([U_o(x=0)/U_o(x=X)]\).
The position of the wall, \(y = 0\), was estimated by observing the output signal from the counter, i.e. after amplifying and filtering, on an oscilloscope. The “wall signal” is very characteristic. The distance from this preliminary wall position was then measured by a dial gauge. Finally, the wall distance was adjusted after the measurements by shifting the velocity curve up or down to make it pass through the origin. This was relatively simple due to the linear relation. The necessary adjustments typically were of the order of 0.02 mm.
Inlet Conditions
The inlet conditions were determined using Pitot tube and LDV-measurements. Mean velocity profiles from Pitot tube measurements, taken at several spanwise positions at and around the spanwise position finally chosen for the main measurements, showed no visible differences in the maximum velocity. There were, however, small differences in the length of the flat parts of the profiles. These are consistent with the earlier statement of a +/-0.1 mm variation in slot height. The variation in the spanwise velocity distribution at \(y = 4.5\) mm was less than +/-0.25%.
LDV measurements of the lower part of the inlet velocity profile were made in order to resolve the boundary layer and to obtain information on the turbulence levels. The boundary layer thickness, defined as \(U = 0.99 U_{max}\), was 1.4 mm. The turbulence intensity in the flat part of the profile was less than 1%. No corrections for gradient broadening was applied to the turbulence measurements, meaning that the peak in turbulence intensity in the boundary layer is exaggerated. We thus have a fairly flat inlet velocity profile with a mean velocity which is uniform in the spanwise direction within +/-0.25%. The flow is laminar and the laminar boundary layers along the walls have a thickness of 1.4 mm.
Persistent spanwise variations of the thickness of the wall jet were noted. These variations are probably associated with the small variation (1%) in slot height. All subsequent measurements were however made at a spanwise position where “average properties” of the wall jet were prevailing.
Available Measurements
The data available includes:
- Profiles of \(U\) and \(u'\) at \(x/b=0\).
- Profiles of \(U\), \(V\), \(u'\), \(v'\) and \(\overline{uv}\) at \(x/b=5\), \(10\), \(20\), \(40\), \(70\), \(100\), \(150\) and \(200\).
- Streamwise development of skin friction coefficient, jet maximum velocity and jet halfwidth.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Streamwise Location | Mean velocity and Reynolds stress profiles |
|---|---|
| \(x/b=0\) | table1.dat |
| \(x/b=5\) | table2.dat |
| \(x/b=10\) | table3.dat |
| \(x/b=20\) | table4.dat |
| \(x/b=40\) | table5.dat |
| \(x/b=70\) | table6.dat |
| \(x/b=100\) | table7.dat |
| \(x/b=150\) | table8.dat |
| \(x/b=200\) | table9.dat |
References
- Bradshaw, P., Gee, M.T. (1960). Turbulent wall jets with and without an external stream. Aeronautical Research Council R&M 3252.
- Buchhave, P. (1975). Biasing errors in individual particle measurements with the LDA-counter signal processor. Proc. LDA-Symposium Copenhagen 1975, Dantec Measurement Technology, Skovlunde, Denmark.
- Buchhave, P. (1979). The measurement of turbulence with the burst-type laser doppler anemometer — errors and correction Methods. Ph.D. Thesis, State University of New York at Buffalo.
- Eriksson, J.G., Karlsson, R.I., Persson, J. (1998). An experimental study of a two-dimensional plane turbulent wall jet. Expts. in Fluids, Vol. 26, pp. 50-60.
- Johnson, D.A., Brown, D. (1990). A laser doppler velocimeter approach for near-wall three-dimensional turbulence measurements, Proc. Fifth Int Symp on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal.
- Karlsson, R.I., Eriksson, J., Persson, J. (1993). An experimental study of a two-dimensional plane turbulent wall jet. Vattenfall Utveckling AB, 1993-12-30.
- So, R.M.C., Speziale, C.G., Launder, B.E. (1993). Near-wall measurements of turbulent structure in boundary layers and wall jets. Near wall turbulent flows.
- Karlsson, R.I., Eriksson, J., Persson, J. (1992). LDV measurements in a plane wall jet in a large enclosure. Proc. 6th International Symposium on Applications of Laser Techniques to Fluid Mechanics, pp.1.5.1-1.5.6.
- Launder, B.E., Rodi, W. (1981). The turbulent wall jet. Prog. Aerospace Sci., Vol. 19, pp. 81—128.
- Morel, T. (1975). Comprehensive design of axisymmetric wind tunnel contractions. J. Fluids Eng., Vol. 977, pp. 225—233.
- Tailland, A., Mathieu, J. (1967). Jet pariétal, Journal de Méchanique, Vol. 6, pp. 103—131.
- Whiffen, M.C. (1975). Polar response of an LV measurement volume, Proc. Minnesota Symposium on Laser Anemometry, University of Minnesota, Minneapolis.
Indexed data:
| case055 (dbcase, semi_confined_flow) | |
|---|---|
| case | 055 |
| title | 2D plane turbulent wall jet |
| author | Karlsson, Eriksson, Persson |
| year | 1991 |
| type | EXP |
| flow_tag | 2d, jet |