Swirling Boundary Layer in a Conical Diffuser
Experiments by Clausen, Koh and Wood
Description
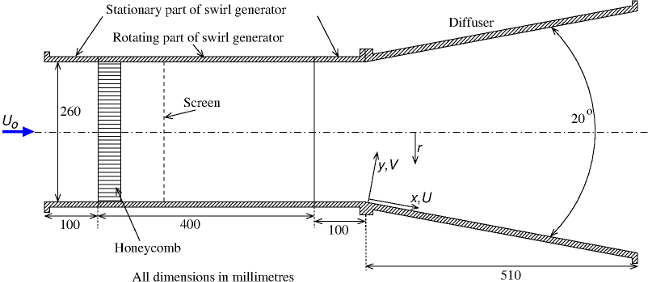
The flow examined is a swirling boundary layer developing in a conical diffuser. The geometry is shown in figure 1. The conical diffuser is placed 100 mm downstream of a rotating swirl generator of diameter \(D=260\) mm and discharges into the atmosphere at \(X=510\) mm. It has a 20o included angle and an area ratio of 2.84.
Flow Characteristics
The swirling flow is created by a rotating cylinder including a honeycomb screen at its inlet. At the outlet of the swirl generator the swirl is close to solid-body rotation, with a reasonably uniform axial velocity in the core region. Along the diffuser, the swirl is of sufficient magnitude to prevent boundary layer separation but just insufficient to cause recirculation in the core flow. The axial pressure gradient and the curvature of the streamlines have been found to be the dominant perturbations imposed to the swirling boundary layer as it exits the cylindrical part and enters the conical diffuser. The swirl is responsible for severe radial gradients near the wall for most of the turbulence quantities.
Flow Parameters
- Air with a kinematic viscosity: \(\nu = 1.5 \times 10^{-5}\) m2/s.
- Average axial velocity at inlet (\(x = -25\) mm): \(U_o = 11.6\) m/s.
- Reynolds number: \(U_oD/\nu = 202,000\).
- Atmospheric pressure at outlet.
Inflow Conditions
Measured profiles of the mean streamwise and swirl velocities, and the Reynolds stresses, are provided at station -25, located at \(x = -25\) mm, which is \(75\) mm downstream of the swirl generator and \(25\) mm upstream of the diffuser entrance. At this location the swirl is close to solid-body rotation with a nearly uniform axial velocity in the core region outside the boundary layers. The swirl number is \(W_{max}/U_o = 0.59\) where \(W_{max}\) is the maximal circumferential velocity. The wall shear stress is \(\tau_{wx}/U_o^2 = 0.00282\) in the \(x\) direction and \(\tau_{wz}/U_o^2 = 0.00190\) in the \(z\) direction. The wall streamline angle is \(\beta_w = \tan^{-1}(W/U)_{y=0} = 34^o\).
Experimental Details
Hot-wire velocity measurements have been carried out using a single wire probe for the mean quantities and an X-wire probe for the turbulence quantities. It has been possible to measure all Reynolds stresses using the technique of rotating the probes +/-45o. It is worth mentioning that the velocity measurements are made in traverses normal to the diffuser wall along the \(y\) axis (\(y\) is perpendicular to \(x\), the coordinate parallel to the wall).
Wall stress \(\tau_w\) was estimated using the logarithmic law of the wall. The two components \(\tau_{wx}\) and \(\tau_{wz}\) were determined using the value of \(\beta_w\).
Static pressure measurements were made using wall taps. The pressure coefficient is defined as \(C_p = 2p/(\rho U_o^2)\).
Measurement Errors
\(\delta(U)\), \(\delta(W)\) : 2%;
\(\delta(\text{Reynolds stresses})\) : 10%;
\(\delta(\text{positions})\): +/-0.01 mm.
Available Measurements
Measurements available include:
- Distribution of the static pressure coefficient along the wall, \(C_p\)
- Profiles perpendicular to the wall of mean velocities \(U\) and \(W\), and all six Reynolds stress components, at eight streamwise locations (one upstream of the diffuser inlet, at \(x=-25\) mm, and 7 along the diffuser, at \(x = 25\), \(60\), \(100\), \(175\), \(250\), \(330\), \(405\) mm)
- Values of the wall shear stresses, \(\tau_{wx}/U_o^2\) and \(\tau_{wz}/U_o^2\), and wall shear angle, \(\beta_w\), at the above 8 locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt gives details of the file naming convention and data available.
Pressure coefficient:
| \(Cp\) along the wall | cp.dat |
|---|
Mean velocities:
| Location | \(U\) and \(W\) profiles, \(\tau_{wx}\), \(\tau_{wz}\) | Normalized \(U\) | Normalized \(W\) |
|---|---|---|---|
| \(x=-25\) mm | mm-25.dat | u-25.dat | w-25.dat |
| \(x=25\) mm | mm025.dat | u025.dat | w025.dat |
| \(x=60\) mm | mm060.dat | u060.dat | w060.dat |
| \(x=100\) mm | mm100.dat | u100.dat | w100.dat |
| \(x=175\) mm | mm175.dat | u175.dat | w175.dat |
| \(x=250\) mm | mm250.dat | u250.dat | w250.dat |
| \(x=330\) mm | mm330.dat | u330.dat | w330.dat |
| \(x=405\) mm | mm405.dat | u405.dat | w405.dat |
Reynolds stresses:
| Location | \(\overline{u^2}\) | \(\overline{v^2}\) | \(\overline{w^2}\) | \(\overline{uv}\) | \(\overline{uw}\) | \(\overline{vw}\) |
|---|---|---|---|---|---|---|
| \(x=-25\) mm | usq-25.dat | vsq-25.dat | wsq-25.dat | uv-25.dat | uw-25.dat | vw-25.dat |
| \(x=25\) mm | usq025.dat | vsq025.dat | wsq025.dat | uv025.dat | uw025.dat | vw025.dat |
| \(x=60\) mm | usq060.dat | vsq060.dat | wsq060.dat | uv060.dat | uw060.dat | vw060.dat |
| \(x=100\) mm | usq100.dat | vsq100.dat | wsq100.dat | uv100.dat | uw100.dat | vw100.dat |
| \(x=175\) mm | usq175.dat | vsq175.dat | wsq175.dat | uv175.dat | uw175.dat | vw175.dat |
| \(x=250\) mm | usq250.dat | vsq250.dat | wsq250.dat | uv250.dat | uw250.dat | vw250.dat |
| \(x=330\) mm | usq330.dat | vsq330.dat | wsq330.dat | uv330.dat | uw330.dat | vw330.dat |
| \(x=405\) mm | usq405.dat | vsq405.dat | wsq405.dat | uv405.dat | uw405.dat | vw405.dat |
Recommendations for Calculations
Calculations should be performed for the whole diffuser (not just for the boundary layer).
It should often be convenient to place the inlet at station \(x=-25\) mm, using the experimental values provided as inlet conditions.
The diffuser discharges to the atmosphere at \(X=510\) mm, where zero gradient conditions may generally be assumed for the flow variables.
Previous Numerical Studies
Armfield et al (1990) used a \(k\)-\(\varepsilon\) and an algebraic Reynolds stress turbulence model with a two-layer wall function to calculate this case. The use of a two-layer, rather than a single-layer, wall function was reported to be necessary to predict the level, location and the axial variation of the near-wall peak in turbulence quantities accurately.
Main References
- Armfield, S.W., Cho, N.H., Fletcher , C.A.J. (1990). Prediction of turbulence quantities for swirling flow in conical diffusers. AIAA J., Vol. 28, p. 453.
- Cho, N.H., Fletcher , C.A.J. (1991). Computation of turbulent conical diffuser flows using a non-orthogonal grid system. Computers and Fluids, Vol. 19, p. 347.
- Clausen, P.D., Koh, S.G., Wood, D.H. (1993). Measurements of a swirling turbulent boundary layer developing in a conical diffuser. Experimental Thermal and Fluid Science, Vol. 6, pp. 39-48.
- Clausen, P.D., Wood, D.H. (1989). The correction of X-Probe results for transverse contamination. Journal of Fluids Engineering, Vol. 111, p. 227.
Indexed data:
| case060 (dbcase, confined_flow) | |
|---|---|
| case | 060 |
| title | Swirling boundary layer in a conical diffuser |
| author | Clausen, Koh, Wood |
| year | 1993 |
| type | EXP |
| flow_tag | axisymmetric, swirl, 3dbl, varying_cross_section |