Turning Flow Over A Flat Plate
Experiment by Müller
Description
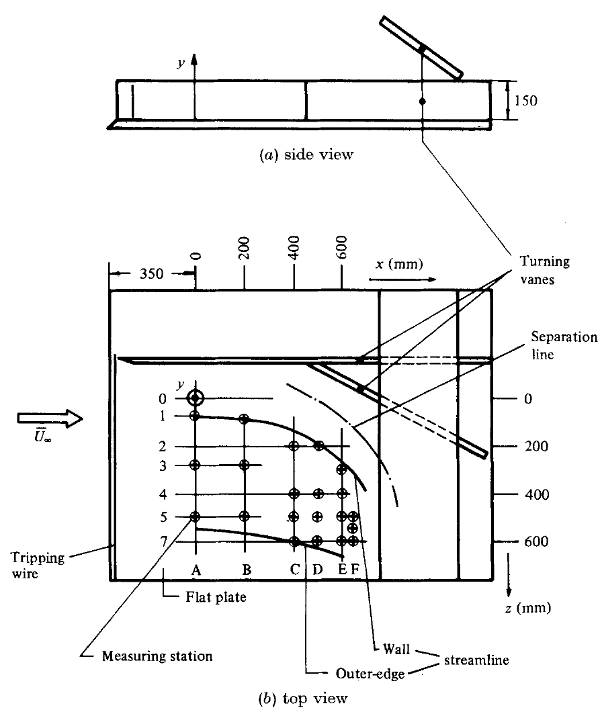
This test case was performed in order to study the steady incompressible, three-dimensional turbulent boundary layer approaching separation. Turning vanes were used to deflect the flow field external to the boundary layer laterally so that streamwise flow deceleration occurred simultaneously with cross-flow acceleration (see figure 1).
Unit Reynolds number: \(Re=1.95 \times 10^6\) m-1
Profiles of the mean velocity components and of the six Reynolds stresses were measured. At each measuring station, the wall shear stress was inferred from a Preston-tube measurement as well as from a Clauser chart.
Geometry
The experiment was carried out in the open test section (length 1.6 m, diameter 1.2 m) of the return-circuit low-speed wind tunnel of the Aerodynamisches Institut.
The three dimensional turbulent boundary layer was developed on a plane smooth Plexiglass plate placed vertically in the test section. A schematic of the experimental set-up, in both side and top view, can be seen in figure 1.
The free stream was deflected with turning angles of up 20o from the initial flow direction by means of turning vanes, thereby imposing a pressure distribution on the boundary-layer flow and causing the wall streamlines to turn by up to 50o. As is shown in figure 1, the boundary layer thickness was artificially increased by tripping the flow with a 5 mm diameter wire attached to the leading edge of the plate.
Measurement Techniques
The measurements were carried out with a goose-neck shape probe support. Single and cross hot-wire probes and pressure probes could be inserted in the holder. The probe support allowed 360o rotation in intervals of 45o so that the complete Reynolds stress tensor could be measured. To carry out the near wall measurements, the probe was inclined at a fixed angle of 10o with respect to the wall.
All measurements were made using DISA 55P11 straight, single-sensor probes and 55P61 cross hot-wire probes.
The yaw angle was measured using the local mean-flow direction, rotating a single normal hot-wire lying tangential to the surface around the \(y\)-axis with angles of \(\pm \Delta \beta = 45^o\) and comparing the hot-wire mean voltage outputs. The line of symmetry found when the wire signals were equal was interpreted as the mean flow direction and defined the local measuring co-ordinate system (\(X_m\), \(Y_m\), \(Z_m\)).
After measuring the yaw distribution throughout the boundary layer, the magnitude of the mean velocities was measured with the probe aligned with the local yaw directions. Measurements were carried out as close to the wall as \(y = 0.1\) mm.
Using a cross hot-wire probe, the velocity components \(U_m\) and \(V_m\) of the total velocity \(U_g\) could be measured with the plane of the wire perpendicular to the wall.
Velocity fluctuations were also measured using the X-wire probe, with the smallest wall distance being \(y = 1.5\) mm.
Before and after each of the 16 r.m.s measurements at one point, the calibration of the hot-wire probe was checked. This was carried out in the free stream behind the wind tunnel nozzle, about 200 mm above the plate.
The Reynolds stress measurements were carried out with cross hot-wire probes rotatable around the longitudinal axis. At each measuring point, the r.m.s. values of both voltage fluctuations as well as those of their sum and difference were measured at four roll angles with intervals of 45o.
The Reynolds stress tensor was evaluated with three different sets of data out of the 16 r.m.s measurements.
Inflow Conditions
Tripped boundary layer with unit Reynolds number \( U_{\infty}/\nu = 1.95 \times 10^6\) m-1
Flow Characteristics
At all measuring stations, the mean velocity profile of the plane spanned by the wall shear-stress vector and the y-axis exhibited a logarithmic wall region, at least over the region \(30 < y^+ < 500\). These measurements compared reasonably well with the law of the wall of two-dimensional flow.
The profiles of the Reynolds stresses were characteristically shaped for boundary-layer flows with adverse pressure gradients. Excluding the measuring stations farthest upstream, the turbulent stresses in the nearly two-dimensional flow have a maximum lying near the wall, as in-zero pressure gradient flow, while in the downstream direction the maximum was shifted away from the surface, corresponding to \(\partial P/\partial x > 0\). The \(\overline{u_m^2}\) component also revealed the same behaviour, yielding large flat maxima at the stations closest to separation. The \(\overline{v_m^2}\) and \(\overline{w_m^2}\) components did not change as much as \(\overline{u_m^2}\). The crosswise Reynolds stress \(\overline{v_mw_m}\) increased markedly in the downstream direction, reaching the same order of magnitude as the \(\overline{u_mv_m}\) stress.
Measurement Errors
The accuracy of the measuring probe position in the \(y\)-direction for a wire lying parallel to the wall was estimated to be +/-0.05 mm.
The accuracy of the measured yaw angles as checked with repeated measurements and different hot-wire probes was about +/-0.5o.
Maximum deviations in the resultant velocity from hot-wire calibration checks of 1% were tolerated.
Using the approximation for evaluating the magnitude of the total velocity vector as described in Müller (1982), the error was below 1.5%.
The relative errors in evaluating the Reynolds stress tensor were about 10%.
The errors in the shear stresses were estimated as 10% of the local streamwise component.
The maximum misalignment between the local velocity vector and the probe axis was 3o, resulting in experimental error of up to 0.5%.
The errors of the wall shear stresses due to pressure gradients were 3%.
Available Measurements
Data available includes:
- Pressure coefficient measurements across the flat plate
- Profiles of mean velocities and Reynolds stresses at the 21 locations indicated in figure 1
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Pressure coefficient measurements | mul-cp.dat |
| Velocity and Reynolds Stress Profiles | |||
|---|---|---|---|
| Station | \(x\) (m) | \(z\) (m) | File |
| A1 | 0 | 0.084 | mul-vel-a1.dat |
| A3 | 0 | 0.284 | mul-vel-a3.dat |
| A5 | 0 | 0.484 | mul-vel-a5.dat |
| B1 | 0.2 | 0.1 | mul-vel-b1.dat |
| B3 | 0.2 | 0.3 | mul-vel-b3.dat |
| B5 | 0.2 | 0.5 | mul-vel-b5.dat |
| C2 | 0.4 | 0.2 | mul-vel-c2.dat |
| C4 | 0.4 | 0.4 | mul-vel-c4.dat |
| C5 | 0.4 | 0.5 | mul-vel-c5.dat |
| C7 | 0.4 | 0.6 | mul-vel-c7.dat |
| D2 | 0.5 | 0.2 | mul-vel-d2.dat |
| D4 | 0.5 | 0.4 | mul-vel-d4.dat |
| D5 | 0.5 | 0.5 | mul-vel-d5.dat |
| D7 | 0.5 | 0.6 | mul-vel-d7.dat |
| E3 | 0.6 | 0.3 | mul-vel-e3.dat |
| E4 | 0.6 | 0.4 | mul-vel-e4.dat |
| E5 | 0.6 | 0.5 | mul-vel-e5.dat |
| E7 | 0.6 | 0.6 | mul-vel-e7.dat |
| F5 | 0.65 | 0.5 | mul-vel-f5.dat |
| F6 | 0.65 | 0.55 | mul-vel-f6.dat |
| F7 | 0.65 | 0.6 | mul-vel-f7.dat |
Reference
- Müller, U.R. (1982). Measurement of the Reynolds stresses and the mean-flow field in a three-dimensional pressure-driven boundary layer. J. Fluid Mech., Vol. 119, pp. 121-153.
Indexed data:
| case065 (dbcase, semi_confined_flow) | |
|---|---|
| case | 065 |
| title | Turning flow over a flat plate |
| author | Muller |
| year | 1982 |
| type | EXP |
| flow_tag | 3d, curvature |