Strained Flow over a Streamwise Axially Rotating Cylinder
Experiments by Bissonnette and Mellor
Description
Mean velocity and mean turbulent field measurements are performed for the case of a three-dimensional turbulent boundary layer on an axially rotated cylinder, as shown in figure 1. The cylinder model consists of two parts: a stationary section followed by a spinning after-body. Techniques of hot-wire anemometry were employed, which yield complete mean velocity and turbulence measurements in skewed flows.
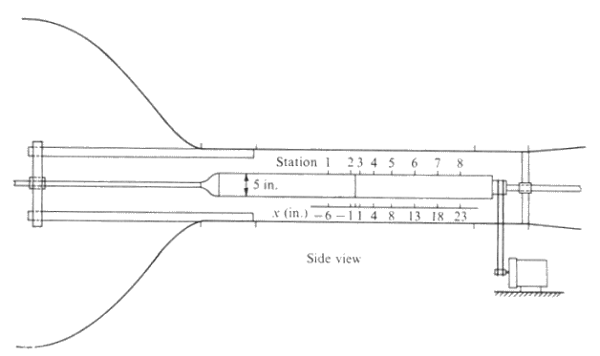 Fig. 1: Schematic diagram of the wind tunnel and model
Fig. 1: Schematic diagram of the wind tunnel and model
The geometry chosen for the present experiment is an axisymmetric turbulent boundary layer skewed by an axially rotated cylinder. Complete mean velocity and turbulence measurements were performed. The cylinder model is made of two sections. The leading stationary section is immediately followed by a rotating section, so that fluid particles, as they enter the zone of influence of the rotating wall, are subjected to a relatively sudden change in mean rate of strain.
Two Reynolds numbers are considered, in both cases with, and without, rotation of the cylinder, as summarized in the table below, where \(U_e\) is the free stream velocity, and \(W_o\) the tangential velocity of the cylinder surface.
| \(U_e\) (ft/s) | \(Re\) | \(W_o\) (ft/s) | \(\Omega\) (\(=W_o/U_e\)) | |
| Low Re | 33.2 | 41,400 | 0 | 0 |
| 59.5 | 1.8 | |||
| High Re | 63.9 | 79,500 | 0 | 0 |
| 59.5 | 0.936 |
Experiment and Apparatus
The experiment consisted of measuring the characteristics of the turbulent boundary layer that develops on a circular cylinder aligned with the mainstream. The cylinder was made of polished aluminium tubing 5 in. O.D. and 0.5 in. thick. It was mounted on a 10ft long ground-steel shaft, rigidly supported at both ends. To minimise disturbances, the forward support was moved upstream, inside the settling chamber.
The model itself was made of two principal sections, each 2.5 ft long. The leading section was stationary, whereas the downstream section was mounted on ball bearings. The gap between the two sections was estimated at 0.002-0.003 in. The rotating cylinder was belt-driven from outside by a 1/4 h.p. constant speed a.c. motor. The rotation speed was measured and constantly monitored by means of a strobe light. It was held constant for all cases reported here and its value was 2800 +/-25 rev/min.
The experiment was carried out in an open return wind tunnel. Figure 1 is a schematic drawing showing the model in place. The air entered through a bell-mouth and passed through seven 24-mesh gauzes and a short settling length before a 20:1 ratio, axisymmetric contraction. The working section was circular, 16 in. diameter and 6 ft long. The air then passed through a diffuser before being exhausted into the atmosphere by an axial flow fan driven by a 5.3 h.p. d.c. motor. The air speed could be varied continuously between approximately 10 and 65 ft/s.
Measurement Techniques
Velocities were measured using hot-wire anemometry with single and X-wire probes.
Measurements Errors
Because of the large contraction ratio of the entrance nozzle, disturbances created by the forward support should be sufficiently reduced. The mainstream turbulence level, with the model in place, was measured to be less than 0.5%. This is not impressively small, but still small enough compared with boundary layer generated turbulence.
The rotation speed was well above the critical frequency of the model of 200rev/min estimated from the observed peak vibrations. At the working speed, vibrations were practically non-existent. Within the accuracy of our traversing mechanism (±0.001 in.), the contact point was found to be the same for both dynamic and static conditions.
Measurements were performed in four different situations. It is recalled that the rotation rate was always kept the same in all cases, but that mainstream velocity was varied instead. Static pressures were recorded on the tunnel walls and not on the model itself, for evident reasons.
Available measurements
Data available include:
- Profiles of mean velocities \(U\) and \(W\) and all six Reynolds stress components at measurement stations 3-8 for the rotating cylinder case at both Reynolds numbers
- Profiles of mean velocity at all measurement stations for the low Reynolds number non-rotating cylinder case
- Profiles of Reynolds stresses at measurement stations 1, 3, 5 and 8 for the high Reynolds number non-rotating cylinder case
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Low Reynolds Number Case | High Reynolds Number Case | ||||
|---|---|---|---|---|---|
| \(\Omega = 0\) | \(\Omega=1.8\) | \(\Omega=0\) | \(\Omega=0.936\) | ||
| Station 1 | Mean velocity | bis-vel-lrn-om0-st1.dat | |||
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om0-st1.dat | bis-str1-hrn-om0-st1.dat | |||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om0-st1.dat | bis-str2-hrn-om0-st1.dat | |||
| Station 2 | Mean velocity | bis-vel-lrn-om0-st2.dat | |||
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | |||||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | |||||
| Station 3 | Mean velocity | bis-vel-lrn-om0-st3.dat | bis-vel-lrn-om1-st3.dat | bis-vel-hrn-om1-st3.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st3.dat | bis-str1-hrn-om0-st3.dat | bis-str1-hrn-om1-st3.dat | ||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st3.dat | bis-str2-hrn-om0-st3.dat | bis-str2-hrn-om1-st3.dat | ||
| Station 4 | Mean velocity | bis-vel-lrn-om0-st4.dat | bis-vel-lrn-om1-st4.dat | bis-vel-hrn-om1-st4.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st4.dat | bis-str1-hrn-om1-st4.dat | |||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st4.dat | bis-str2-hrn-om1-st4.dat | |||
| Station 5 | Mean velocity | bis-vel-lrn-om0-st5.dat | bis-vel-lrn-om1-st5.dat | bis-vel-hrn-om1-st5.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st5.dat | bis-str1-hrn-om0-st5.dat | bis-str1-hrn-om1-st5.dat | ||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st5.dat | bis-str2-hrn-om0-st5.dat | bis-str2-hrn-om1-st5.dat | ||
| Station 6 | Mean velocity | bis-vel-lrn-om0-st6.dat | bis-vel-lrn-om1-st6.dat | bis-vel-hrn-om1-st6.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st6.dat | bis-str1-hrn-om1-st6.dat | |||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st6.dat | bis-str2-hrn-om1-st6.dat | |||
| Station 7 | Mean velocity | bis-vel-lrn-om0-st7.dat | bis-vel-lrn-om1-st7.dat | bis-vel-hrn-om1-st7.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st7.dat | bis-str1-hrn-om1-st7.dat | |||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st7.dat | bis-str2-hrn-om1-st7.dat | |||
| Station 8 | Mean velocity | bis-vel-lrn-om0-st8.dat | bis-vel-lrn-om1-st8.dat | bis-vel-hrn-om1-st8.dat | |
| \(\overline{u^2}\), \(\overline{w^2}\), \(\overline{uw}\) stresses | bis-str1-lrn-om1-st8.dat | bis-str1-hrn-om0-st8.dat | bis-str1-hrn-om1-st8.dat | ||
| \(\overline{v^2}\), \(\overline{uv}\), \(\overline{vw}\) stresses | bis-str2-lrn-om1-st8.dat | bis-str2-hrn-om0-st8.dat | bis-str2-hrn-om1-st8.dat | ||
| Skin friction gradient at Stations 5,6,7,8 | bis-lrn-ut-grd.dat | bis-hrn-ut-grd.dat | |||
References
- Bissonnette, L.R., Mellor, G.L. (1974). Experiments on the behaviour of an axisymmetric turbulent boundary layer with a sudden circumferential strain. J. Fluid Mech., Vol. 63, pp. 369-413.
Indexed data:
| case066 (dbcase, semi_confined_flow) | |
|---|---|
| case | 066 |
| title | Strained flow over a streamwise axially rotating cylinder |
| author | Bissonnette, Mellor |
| year | 1974 |
| type | EXP |
| flow_tag | axisymmetric, 3dbl |