Flow over Isolated 2D Valley
Experiments by Khurshudyan, Snyder, Nekrasov, Lawson, Thompson and Schiermeier
Description
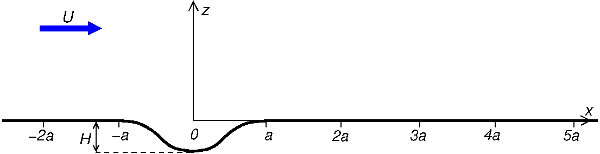
The case consists of flow over an isolated 2D valley in a neutral boundary layer, as shown schematically in figure 1. The free-stream velocity \(U_{\infty} = 4\) m/s. Three valley geometries are considered, each of maximum depth \(H = 0.117\) m, but with different lengths, giving aspect ratios \(a/H\) of 3, 5 and 8.
Wind Tunnel
The wind tunnel test section was 3.7 m wide, 2.1 m high and 18.3 m long. The air speed in the test section could be varied from 0.5 to 10 m/s. An instrument carriage, supported on rails along the test-section walls, was capable of positioning a probe or sampling rake by manual or computer-aided control. An atmospheric boundary layer was simulated by placing a fence (vertical barrier) of 153 mm height at the entrance to the test section and covering the tunnel floor downwind of the fence with rough gravel. The gravel, consisting of stones of approximately 10 mm and smaller diameter, was epoxy-cemented onto plywood floor panels. Previous tests showed that an equilibrium boundary layer (i.e., very slowly developing) that is a reasonable approximation to the neutral atmospheric boundary layer was established at a distance of 7 to 8 m downstream of the fence (Arya and Shipman, 1981; Arya et al., 1981). Additional measurements of the boundary-layer structure and dispersion characteristics were made during the current study. The ceiling height of the wind tunnel was adjusted to ensure a longitudinal pressure gradient of zero over the flat terrain. It was not readjusted when the model valleys were installed.
The Models
Three model valleys were constructed; all had shapes given parametrically for \(|\xi| \le a\) by
\[ x(\xi) = 0.5\xi \left[ 1 + \frac{a^2}{\xi^2 + m^2 (a^2 - \xi^2)} \right] \] \[ z(\xi) = -0.5m (a^2 - \xi^2)^{1/2} \left[ 1 - \frac{a^2}{\xi^2 + m^2(a^2 - \xi^2)} \right] \]
where \(m = (H/a) + \left[ (H/a)^{2} + 1 \right]^{1/2}\).
\(H\) is the height (depth) of valley, \(a\) the half-width of valley, and \(\xi\) is an arbitrary parameter. \(x\) is directed along the approach flow direction (origin at centre of valley), and \(z\) is directed vertically upward. Since the surface is two-dimensional, the equations do not include the \(y\) variable, and the models extended across the width of the test section of the wind tunnel. These valley shapes are smooth, symmetric about the \(z\)-axis, and smoothly merge into a flat plane at the points \(x = \pm a\). They describe a two-parameter family of surfaces, the parameters being \(h\) and the aspect ratio \(n = a/h\).
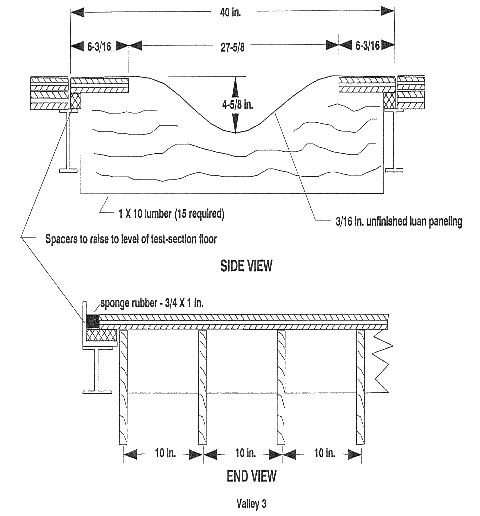
The valleys constructed for this study had aspect ratios of 3, 5, and 8 (maximum slopes of 26o, 16o, and 10o respectively). All had heights of 117 mm and, therefore, half-widths of \(a = 351\) mm, \(585\) mm, and \(936\) mm. figure 2 shows the construction details of the three valleys. The actual shapes differed from the ideal ones by less than +/-5 mm. All the models were covered with gravel to match the roughness of the wind-tunnel floor. The difference between the ideal and actual shapes was due primarily to the uncertainty in measuring to the top of the gravel roughness. The leading edges of all the valleys were placed 8 m downwind of the fence at the entrance to the test section.
Experimental Details
Two basic types of instruments were used to measure the flat-terrain boundary layer and the flow structure within the valleys, a hot-wire anemometer (HWA) and a pulsed-wire anemometer (PWA). In valley 8, where indicated turbulence intensities were generally less than 25%, the HWA was used for the bulk of the measurements. In valleys 3 and 5, however, the flows were highly turbulent and reversing, so the HWA measurements within the valley were supplemented with PWA measurements. The hot-wire probes were calibrated against a Pitot-static tube mounted in the free-stream of the wind tunnel above the boundary layer (typically at a height of 1200 mm above the floor). These calibrations were checked at least once each day and recalibrations were made as deemed necessary. The PWA probe can be oriented to measure the velocity components in all three co-ordinate directions. Because of the finite wire lengths, the probe has a yaw response up to about 700, so that, for reasonable measurements of transverse components of the flow, the turbulence intensity must be relatively high, e.g., above 20 to 25%.
A large amount of information was collected on the flow structure over the valleys. In general, measurements were made at a number of locations (longitudinal positions) from \(x/a = -2.0\) to \(x/a \ge 5.0\) for each valley. HWA measurements were made with the uw-probe at several longitudinal positions in flat terrain and at all locations for each valley. A complete set of HWA measurements was made with the uv-probe over valley 8 only. Approximately 75 individual profiles were measured with the HWA, each profile consisting of approximately 20 measurement points. Each measurement provided information on the mean velocity, the angle of the mean velocity, two components of turbulence intensity (\(u\) and \(w\) or \(u\) and \(v\)), and Reynolds shear stress. The HWA measurements were supplemented by PWA measurements within the high-turbulence regions in the valleys. Approximately 60 PWA profiles were measured, each profile consisting of approximately 10 points. Each measurement provided information on the mean velocity, the turbulence Intensity, and the skewness and kurtosis of the velocity distributions Additionally, time-series data were recorded at several elevations above each of the valley centres (a total of about 40 time series). These data were analysed to obtain more detail on the nature of the velocity fluctuations; that is, the probability density distributions were annualised from each of these time series.
Available measurements
Profiles are available for the three different aspect ratio valleys (\(a/H=3\), \(5\) and \(8\)) at a number of \(x\)-locations. Some profiles are also provided for the baseline flat plate case (without the valley). Quantities available include:
- the mean velocity \(U\) (in m/s)
- flow angle \(\phi\) (in degrees)
- rms fluctuating axial and vertical velocities (\(u'\) and \(w'\)) (in m/s)
- rms transverse velocity \(v'\) for the \(a/H=8\) case
- Reynolds shear stress \(-\overline{uw}\) (in (m/s)2)
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Baseline Flat Plate Case | |
|---|---|
| Location | File |
| \(x=-1.075\) m | epanv1s.dat |
| \(x=-0.175\) m | epanv2s.dat |
| \(x=0.475\) m | epanv3s.dat |
| \(x=3.825\) m | epanv4s.dat |
| \(x=7.025\) m | epanv5s.dat |
| Location | \(a/H=3\) Case | \(a/H=5\) Case | \(a/H=8\) Case |
|---|---|---|---|
| \(x=-2a\) | epav301s.dat | epav501s.dat | epav801s.dat |
| \(x=-1.25a\) | epav302s.dat | epav502s.dat | epav802s.dat |
| \(x=-a\) | epav303s.dat | epav503s.dat | epav803s.dat |
| \(x=-0.75a\) | epav304s.dat | epav504s.dat | epav804s.dat |
| \(x=-0.5a\) | epav305s.dat | epav505s.dat | epav805s.dat |
| \(x=-0.25a\) | epav306s.dat | epav506s.dat | epav806s.dat |
| \(x=0\) | epav307s.dat | epav507s.dat | epav807s.dat |
| \(x=0.25a\) | epav308s.dat | epav508s.dat | epav808s.dat |
| \(x=0.5a\) | epav309s.dat | epav509s.dat | epav809s.dat |
| \(x=0.75a\) | epav310s.dat | epav510s.dat | epav810s.dat |
| \(x=a\) | epav311s.dat | epav511s.dat | epav811s.dat |
| \(x=1.25a\) | epav312s.dat | epav512s.dat | epav812s.dat |
| \(x=2a\) | epav313s.dat | epav513s.dat | epav813s.dat |
| \(x=3a\) | epav314s.dat | epav514s.dat | epav814s.dat |
| \(x=5a\) | epav315s.dat | epav515s.dat | epav815s.dat |
| \(x=8.6a\) | epav516s.dat | ||
| \(x=15a\) | epav316s.dat |
References
- Khurshudyan, L.H., Snyder, W.H., Nekrasov, I.V., Lawson, R.E., Thompson, R.S., Schiermeier, F.A. (1990). Flow and dispersion of pollutants within two-dimensional valleys. U.S. Env. Prot. Agcy. Rpt. No. EPA-600/4-79-051. Res. Tri. Pk., NC.
Indexed data:
| case070 (dbcase, semi_confined_flow) | |
|---|---|
| case | 070 |
| title | Flow over isolated 2D valley |
| author | Khurshudyan, Snyder, Nekrasov, Lawson, Thompson, Schiermeier |
| year | 1991 |
| type | EXP |
| flow_tag | 2d, separated |