Turbulent Pipe Flow with Swirl
Experiments by Steenbergen
Description
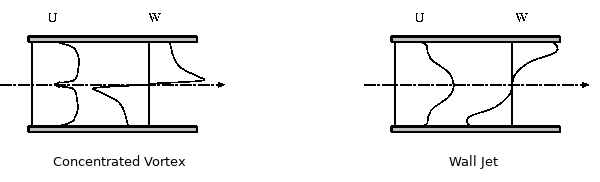
Water flows along a straight pipe are considered with two types of swirl: “wall jet” (WJ hereafter) and “concentrated vortex” (CV hereafter), as shown in figure 1. These names are based on the initial conditions of the measurement series.
The pipe diameter is \(D=70\) mm, and the pipe wall is hydraulically smooth.
For each of the initial conditions WJ and CV, two Reynolds numbers have been considered: \(Re_D=50,000\) and \(300,000\), based on the bulk velocity (measured with a magnetic flowmeter) and on the pipe diameter \(D=70\) mm.
Profiles of mean velocity and Reynolds stresses have been measured at a number of streamwise locations up to \(x/D\) of 75 or greater.
Measurement Techniques
The data have been obtained with a 2-component laser-Doppler system, the fluids being water. The total velocity vector and Reynolds stress tensor have been obtained by performing three measurements in each point, with the laser-Doppler system aligned under three different angles within the azimuthal plane, i.e. the plane perpendicular to the pipe axis. See chapters 3 and 4 of Steenbergen (1995).
Available measurements
The data contain profiles of mean velocities and Reynolds stresses at a number of streamwise locations for each flow case.
Sample plots of selected quantities are available.
All data are presented in nondimensional form: mean velocities are scaled with the bulk velocity, Reynolds stresses are scaled with the bulk velocity squared. Radial positions (measured from the pipe axis) are scaled with the pipe radius \(R\), while the axial positions of the measurement planes are scaled with the pipe diameter \(D\). The data are expressed in a cylindrical coordinate system, with the velocity components into the axial, azimuthal and radial direction denoted by \(U\), \(W\) and \(V\), respectively.
The filenames consist of 6 or 8 characters, and the extension .dat. The 6 or 8 characters have the following meaning:
| 1: | type of initial condition: “w” = WJ, “c” = CV |
|---|---|
| 2: | Reynolds number \(Re_D\): “5” = 50,000; “3” = 300,000 |
| 3: | quantity: “m” = mean velocity; “r” = Reynolds stress |
| 4..6: | distance from reference plane, expressed in \(x/D\) (times 10) |
| 7..8: | Optional. Reference to angle of traversing line, for data not taken on the horizontal plane. |
For example, file c5r043.dat contains the Reynolds stresses at \(x/D=4.3\), for the “concentrated vortex” at a Reynolds number of 300,000. The file named w5m552a1.dat refers to the “wall jet”, \(Re_D=50,000\), \(x/D=55.2\), mean velocities, measured along a line under angle with the horizontal direction (positive in the anticlockwise sense), referred to as a1 in the table below. The following non-zero angles of the traversing lines have been used:
| name | a1 | a2 | a3 | a4 | a5 |
|---|---|---|---|---|---|
| angle (o) | 5 | -65 | 17 | -73 | -67 |
A few of the mean velocity files contain additional data points in a denser grid, see fig. 5.5 of Steenbergen (1995). These points have been placed below the columns of the other data points in the files. grid.
The data can be downloaded as compressed archives from the links below, or as individual files.
References
- Steenbergen, W. (1995). Turbulent pipe flow with swirl. PhD Thesis, Eindhoven University of Technology.
Indexed data:
| case072 (dbcase, confined_flow) | |
|---|---|
| case | 072 |
| title | Turbulent pipe flow with swirl |
| author | Steenbergen |
| year | 1995 |
| type | EXP |
| flow_tag | axisymmetric, swirl, constant_cross_section |