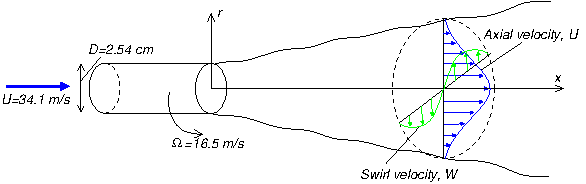
Single-Stream Swirling Jet in Still Air
Experiments by Morse
Description
Single-stream swirling jet in still air.
Swirl number: \(S = G_{\theta}/(RG_{x}) = 0.36\) where \(G_x\) and \(G_{\theta}\) are the axial and angular momentum fluxes, and \(R\) the incoming pipe radius.
Exit Reynolds number: \(Re = 56,000\)
Introduction
The addition of swirl has large-scale effects on free jet development. In particular, the rate of mixing in-creases with swirl intensity. Thus swirling jets spread more quickly, and the mean velocities decay more rapidly than in a non-swirling jet. In a strongly swirling jet the gradients of static pressure set up across the flow field introduce adverse axial pressure gradients in the region of swirl decay, and these may be strong enough to cause reversal of the forward velocities near the jet axis. Thus a re-circulation zone is set up downstream of the jet orifice. Weaker swirl leads to less strong curvature of the stream lines, and the flow is then amenable to analysis as a thin shear layer. Even so, the spreading rate may reach as much as twice that of a non-swirling jet. The enhanced mixing resulting from the adverse pressure gradient leads to increases in the turbulence intensities. Further downstream, where the swirl field is weakened, the turbulence levels and the spreading rate reduce approximately to those of the non-swirling jet.
In this experiment values of \(U\), \(V\), \(W\) and all \(\overline{u_iu_j}\) were measured for swirl numbers: \(S = 0\) and \(S = 0.36\) for downstream distances up to \(x/D = 6\). The external field was stationary. This test case involves the theoretical and experimental comparison between the variation of the centre-line values of \(U\), \(\overline{u^2}\) and \(\overline{v^2}\) with \(x/D\), as well as the decay of the maximum swirl velocity.
Experimental Summary
For comparison, a number of experimental investigations of free-swirling flows, including the present one, are summarized in the table below.
| Author(s) | Method of Swirl Generation | Measurement Technique | Range of Axial Distance | Range of Swirl Number | Recirculation? | Measured Quantities |
|---|---|---|---|---|---|---|
| Rose (1962) | rotating pipe | hot-wire | 0.235-15.0 | 0-0.23 | No | \(U\), \(V\), \(W\), all normal stresses |
| Chigier and Beer (1964) | tangential ports | impact probe | 0-0.6 | 0.39-1.43 | Yes | \(U\), \(W\) |
| Keer and Fraser (1965) | vanes | impact probe | 11.7-19.0 | 0-0.72 | No | \(U\), \(V\), \(W\) |
| Chigier and Chervinsky (1967) | tangential ports | impact probe | 1.0-15.0 | 0.13-0.66 | Yes | \(U\), \(W\), \(P\) |
| Mathur and MacCallum (1967) | vanes | impact probe | 0.6-20.0 | 0-2.7 | Yes | \(U\), \(W\), \(P\) |
| Maier (1967) | vanes | impact probe | 0.27-30.0 | 1.75-2.9 | Yes | \(U\), \(W\) |
| Craya and Darrigol (1967) | tangential ports | hot-wire | 1.0-15.0 | 0-1.58 | Yes | \(U\), \(V\), \(W\), all \(\overline{u_iu_j}\) |
| Syred, Beer and Chigier (1971) | tangential ports | hot-wire | 0-2.0 | 2.2 | Yes | \(U\), \(W\), \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\), \(\overline{uw}\) |
| Kawaguchi and Sato (1971) | tangential ports | hot-wire | 0.1-4.0 | 0.6-0.9 | Yes | \(U\), \(W\), \(P\), all normal stresses |
| Pratte and Keffer (1972) | rotating pipe | hot-wire | 1.0-30.0 | 0.3 | No | \(U\), \(W\), all \(\overline{u_iu_j}\) |
| Hösel (1978) | tangential ports | LDA | 0.25-40.0 | 0-1.7 | Yes | \(U\), \(V\), \(W\) all \(\overline{u_iu_j}\) |
| Fornoff (1978) | tangential ports | LDA | 0.25-40.0 | 0.53 | No | \(U\), \(V\), \(W\) all \(\overline{u_iu_j}\) |
| Hellat (1979) | tangential ports | hot-wire; impact probe | 0.56-2.79 | 0-2.28 | Yes | \(U\), \(V\), \(W\) all \(\overline{u_iu_j}\) |
| Ribeiro and Whitelaw (1980) | tangential ports | hot-wire | 0-6.0 | 0.32 | No | \(U\), \(V\), \(W\) all \(\overline{u_iu_j}\) |
| Morse (1980a) | tangential ports | hot-wire | 0.5-20.0 | 0-0.40 | No | \(U\), \(V\), \(W\) all \(\overline{u_iu_j}\) |
Available Measurements
Measurements available for the swirling case include:
- Development of centreline velocity, maximum swirl velocity and jet halfwidth along the jet.
- Profiles of mean velocity and Reynolds stress components at six streamwise locations: \(x/D=0.5\), \(1\), \(2\), \(4\), \(6\) and \(10\).
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
morse0.dat contains the development of centreline velocity, maximum swirl velocity and jet halfwidth along the jet. The files containing cross-jet profiles are given in the table below.
| Streamwise location | File |
|---|---|
| \(x/D=0.5\) | morse1.dat |
| \(x/D=1.0\) | morse2.dat |
| \(x/D=2.0\) | morse3.dat |
| \(x/D=4.0\) | morse4.dat |
| \(x/D=6.0\) | morse5.dat |
| \(x/D=10.0\) | morse6.dat |
References
- Chigier, N.A., Beer, J.M. (1964). Velocity and static pressure distributions is swirling air jets issuing from annular and divergent nozzles. ASME J. Basic Eng., Vol. 86, p. 788.
- Chigier, N.A., Chervinsky, A. (1967). Experimental investigation of swirling vortex motions in jets. ASME J. Appl. Mech., Vol. 89, p. 443.
- Craya, A., Darrigol, M. (1967). Turbulent swirling jet. Phys. Fluids, Vol. 34, pp. S197-S199.
- Fornoff, M. (1978). Experimentelle une Theoretische Untersuchung von Drallstrahlen. Diplomarbeit, Univ. of Karlsruhe.
- Keer, N.M., Fraser, D. (1965). Swirl, Part I: Effect on axisymmetric turbulent jets. J. Inst. Fuel, Vol. 38, p. 519.
- Gibson, M.M., Younis, B.A. (1986). Calculation of swirling jets with a Reynolds stress closure. Phys. of Fluids, Vol. 29, p. 38.
- Hellat, J. (1979). Turbulente Strömung und Mischung in Erdgas-Diffusionsflammen mit Luftdrall. PhD Thesis, Univ. of Karlsruhe.
- Hösel, W. (1978). Drallstrahlenuntersuchengen mit einem Weiterentwickelten-Laser-Doppler Messverfahren. Rep. SFB 80/E/120, Univ. of Karlsruhe.
- Kawaguchi, D., Sato, D.T. (1971). Experimental investigation of premixed swirling jet flames:velocity and turbulence intensity of swirling air jets. Bull. JSME, Vol. 14, p. 248.
- Maier, P. (1968). Untersuchung isothermer drallbehafteter Freistrahlen. Forsch. Ingenieurwes., Vol. 34, pp. 133-140.
- Mathur, M.L., MacCallum, N.R.L (1967). Swirling air jets issuing from vane swirlers. Part 1: free jets. J. Inst. Fuel, Vol. 214, pp. 214-225.
- Morse, A.P. (1980). Axisymmetric free shear flows with and without swirl. PhD Thesis, Imperial College of Science and Technology, University of London.
- Pratte, B.D., Keffer, J.F. (1973). The turbulent swirling jet. ASME J. Basic Eng., Vol. 94, p. 739.
- Ribeiro, M.M., Whitelaw, J.H. (1976). Turbulent mixing of coaxial jets with particular reference to the near-exit region. ASME J. Fluids Eng., Vol. 981, p. 284.
- Syred, N., Beer, J.M., Chigier, N.A. (1971). Turbulence measurements in swirling recirculating flows. Proc. Symp. on Internal Flows, Univ. of Salford.
Indexed data:
| case026 (dbcase, free_flow) | |
|---|---|
| case | 026 |
| title | Single-Stream Swirling Jet in Still Air |
| author | Morse |
| year | 1980 |
| type | EXP |
| flow_tag | axisymmetric, jet, swirl |