Stably-Curved Mixing Layer
Experiments by Castro and Bradshaw
Description
As part of a general investigation of complex turbulent flows, extensive one-point measurements have been made of the turbulence structure of the mixing layer bounding a normally impinging plane jet with an irrotational core. The ratio of shear-layer thickness to streamline radius of curvature reaches a maximum of about 0.2, the sense of the curvature being stabilizing. Downstream of the impingement region tile shear layer returns asymptotically to being a classical plane mixing layer.
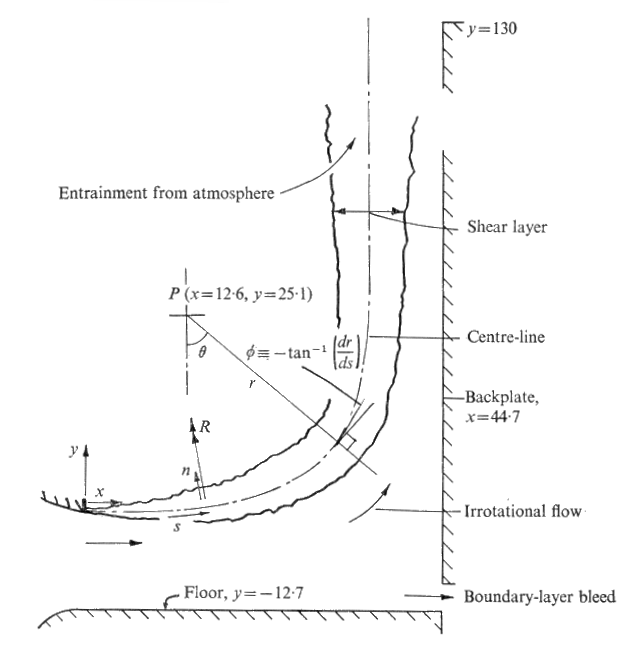
The configuration chosen for the present experiments is shown in figure 1; the maximum value of \(\partial V/\partial x\) in the central region of the mixing layer is about \(-0.2\partial U/\partial y\), using \(x\), \(y\) axes aligned with the local direction of the shear layer, so that the 'fairly thin shear layer' limit is exceeded for a short streamwise distance only. The flow can be thought of as half a two-dimensional impinging jet, with a potential core; the 'floor' replaces the plane of symmetry. It was chosen as the only obvious case of a monotonic shear layer (i.e. one with mean shear of the same sign everywhere) which could be strongly perturbed by a short region of large curvature without the occurrence of a change of species (e.g. a change from a free jet to a wall jet or from a boundary layer to a separated shear layer). Two disadvantages of the present configuration are that only a stabilizing sense of streamline curvature can be obtained and that the mixing layer merges with the boundary layer on the impingement surface before relaxation to the self-preserving state is complete. The second disadvantage is minor, since we documented the self-preserving plane mixing layer in a companion experiment; the first is outweighed by the clarity with which (stabilizing) curvature effects are demonstrated by this flow, and by the practical importance of impinging jet flows.
The measurements presented here were intended to document the transport equations for turbulent energy and shear stress as fully as possible, and include the triple products that effect turbulent transport of shear stress and turbulent energy. We have not measured any quantities involving pressure fluctuations, and our deductions of energy dissipation rates from frequency spectra may not be absolutely reliable, although they should be adequate for comparative purposes. The unmeasured pressure-strain 'redistribution' term in the shear-stress transport equation can be deduced as the difference in the measured terms if transport by pressure fluctuations can be neglected: this neglect seems to be justified except near the high velocity edge of the curved shear layer. So far, only one-point measurements have been made, but the results emphasize the need for correlation measurements to provide information about eddy length scales.
Measurement Details
Velocities measured with constant-temperature anemometers, single-wire probes and cross-wire probes.
Apparatus and Techniques
The rig shown in figure 1 was attached to the exit nozzle of a \(30\times 5\) in. (\(7.6\times 12.7\) cm) blower tunnel. The tunnel turbulence level, measured within a conventional working section, was less than 0.09% at the exit speed, \(U_{ref}\) or \(U_r\), of 100 ft/s (33 m/s) used in the present experiments. Measurements in a plane mixing layer at the same tunnel speed, presented in detail by Castro (1973), showed that mean velocity profiles were accurately self-preserving for \(x > 20\)cm (\(U_{ref}x/\nu = 4\times 10^5\), \(x/\theta_o \approx 700\)) with a spreading parameter \(\sigma\) of 11.1.
The ratio of the distance of the nozzle from the impingement surface, 4.47 cm, to the height of the nozzle opening, 12.7cm, was chosen such that the core of irrotational flow would not be completely entrained by the shear layer until well after the end of the curved region. Boundary-layer separation in the corner between the floor and the impingement surface (the 'backplate' in figure 1) was suppressed by allowing a volume flow of air equal to about \(4 U_{ref}\) cm3/s per unit span to escape through a slot in the corner running the full width of the test rig.
The potential-flow streamlines cannot be calculated from the rig geometry, and a reference streamline was therefore measured. An electrically heated wire was fixed along a spanwise line 4 cm below the upper lip of the nozzle (\(y = - 4\) cm in figure ) and the path of the streamline starting at the wire was traced by traversing a thermocouple normal to the heated wake. This streamline remains in the potential flow until after the end of the curved region, and thereafter the backplate surface was used as the reference streamline. Two-dimensionality of the shear layer was checked by measuring the spanwise distance between the thermal wakes of two heated wires set normal to the plane of the layer near the nozzle lip. The flow diverged slightly: a pessimistic estimate of the apparent origin of lateral divergence was about 20 m upstream of the nozzle lip, corresponding to an error in momentum balance of no more than 3%, and divergence was therefore ignored in analysing the results. Standard hot-wire techniques were used, with DISA 55D01 constant-temperature anemometers, 55F01 single-wire probes and 55A38 cross-wire probes. Probes were individually calibrated for response to the magnitude and direction of the velocity.
The yaw calibrations of the cross-wire probes were expressed as the apparent angle between the wire and the stream, deduced from the calibration by assuming that the wire responded only to the velocity component normal to itself. In effect, this fits the yaw calibration by a cosine curve with the same slope over the (small) range of calibration and uses the cosine as a plausible extrapolation (Bradshaw 1971, pp.121 ff.). The geometrical angle of the wire is not required. The problems of yaw calibration are discussed at greater length by Castro (1973), where it is concluded that the inevitable inaccuracies resulting from the inability of a 45o wire to distinguish between flow angles of \(45 - \theta\) and \(45 + \theta\) render the use of calibrations more elaborate than the 'effective cosine' law rather unrealistic.
The digital processing techniques are straightforward, with the exception of the determination of the intermittency. The problems that appear in the latter, which are largely ignored by the 'eyeball' process of finding intermittency from oscilloscope traces and suppressed by the heavily damped analog intermittency meters used by many workers in the past, are discussed in more detail by Castro (1973) and Bradshaw & Murlis (1974). In the present work the flow was declared turbulent when \(\partial(uv)/\partial t\) or \(\partial^2(uv)/\partial t^2\) exceeded a chosen threshold value, ignoring turbulent or irrotational intervals of less than two digital sampling intervals (0.2 ms, or a distance of 0.40 cm in the maximum- intensity region, where \(U = 20\)m/s. Measurements in a boundary layer by Murlis (unpublished) show that the probability density of 'burst' length rises monotonically as the burst length decreases, at least down to the shortest measurable length: deductions about an average burst length are therefore essentially unreliable and are not attempted here.
Available Measurements
The data available include profiles of mean velocity and Reynolds stresses across both the curved section of the mixing layer and the downstream straight section.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
There are four files:
- f0331a-part-1.dat : Mean flow measurements in the curved section, using offset polar coordinates with the origin at point P in figure 1 (\(x=12.6\) cm, \(y=25.1\) cm).
- f0331a-part-2.dat : Turbulence measurements in the curved section, using offset polar coordinates as for part 1.
- f0331a-part-3.dat : Mean flow and turbulence measurements in the straight downstream section, using Cartesian coordinates.
- f0331a-part-4.dat : Definition of the “reference streamline” as explained in the Measurement Details above.
References
- Castro, I.P., Bradshaw, P. (1976). The turbulence structure of a highly curved mixing layer. J. Fluid Mech., Vol. 73, p. 265.
Indexed data:
| case024 (dbcase, free_flow) | |
|---|---|
| case | 024 |
| title | Stably Curved Mixing Layer |
| author | Castro, Bradshaw |
| year | 1976 |
| type | EXP |
| flow_tag | 2d, mixing_layer, curvature |