Low Reynolds Number Turbulent Flow Near Wakes
Experiment by Gough and Hancock
Description
Measurements have been made in two low-Reynolds number wakes, one symmetrical and one asymmetrical with a boundary layer thickness ratio of 1.9.
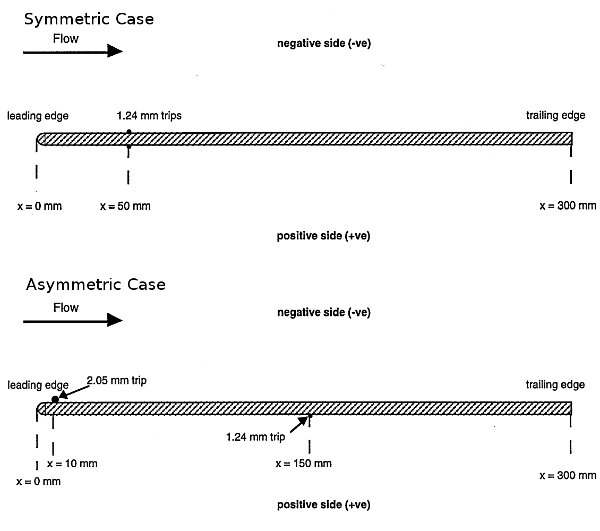
The wake are formed behind a flat plate, 300 mm long, with a trailing edge thickness of 0.96 mm (approximately 0.1 times the boundary layer thickness near the trailing edge). As shown in figure 1, for the symmetric case the boundary layers were tripped symmetrically on the upper and lower surfaces of the plate, whereas for the asymmetric case the trip sizes and locations were different on the two surfaces.
The geometry and flow conditions were matched as closely as possible to a large eddy simulation study using a rectangular variable density mesh. If the smallest mesh size is to remain an acceptable multiple of the smallest scales the computation time will increase with Reynolds number roughly as (\(U_e\theta/\nu)^3\), where \(\theta\) is the momentum thickness and \(U_e\) the free-stream velocity. It was decided that \((U_e\theta/\nu)\) should not exceed about 600. Given that turbulence is only naturally sustainable for Reynolds numbers greater than about 300 this Reynolds number range imposed severe constraints on the experiments, in particular the tripping of the boundary layer so as to be free of residual trip effects.
The trailing edge thickness, \(t\), was about 0.1 of the boundary layer thickness, \(\delta\), at the trailing edge. This is larger than typical of an aircraft wing but comparable to that of a wing element or blade.
Experimental Details
The wake was developed from the trailing edge of a flat plate, 300mm long, 600mm span and 0.96mm thick, the largeness of the span permitting the measurements to extend in to the far wake sufficiently free from end-flow effects. The plate length and free-stream velocity is a compromise; at 10m/s the boundary-layer thickness is about 9mm, for \(U_e\theta/\nu = 600\). Decreasing the free-stream velocity (inversely) increases the boundary layer thickness, thereby reducing probe resolution volume and position errors, but requires probe calibration over a lower velocity range and measurement of still smaller (inversely squared) wall shear stress. The free-stream velocity was 9.6m/s, and the pressure gradient was negligible. The boundary layer was tripped by means of a round wire finely glued to the plate surface. Its size was found to be crucial in terms of providing the correct amount of stimulation and, contrary to the suggestions in the literature, strongly dependent on the upstream laminar boundary layer thickness when this was relatively thick.
Hot-wire measurements were made by means of single-wire and sub-miniature x-wire probes. No wire-length effects were observed for single-wire measurements for lengths less than 1.0mm. The sensors of the cross-wire probes were nominally 0.45mm long separated by about 0.5mm.
Measurement Errors
Probe resolution errors were shown to have been small, even in the regions of the large stress gradients immediately downstream of the trailing edge. Wall shear stress was measured using Preston tubes, and by fitting the velocity profile to the logarithmic law. It is now well demonstrated (e.g. Erm and Joubert, 1991) that the logarithmic law is not Reynolds number dependent at low Reynolds numbers. The Preston tube technique requires the existence of an inner-layer law, and the calibration is implied by this law; self consistency from tubes of differing diameters and with that inferred from the velocity profile therefore implies the existence of the inner-layer form. Agreement in friction velocity \(u_{\tau}\) was within +/-1.6%.
Available Measurements
Data available includes:
- Development of wake widths, and integral parameters along the flow direction
- Profiles of mean velocity, Reynolds stresses, and some higher order moments at selected streamwise locations
- Development of mean velocity, Reynolds stresses and some higher order moments along the centreline
- Budgets of \(k\) and \(\overline{uv}\) at selected locations for the symmetric wake case
- Spectra of \(u'\) at selected locations for both cases.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Symmetric Wake | Asymmetric Wake | |
|---|---|---|
| Overview/summary of data files | symread-me.txt | asymread-me.txt |
| Wake thicknesses and integral parameters | sips.dat | aips.dat |
| Profiles across the wake (Mean velocity, Reynolds stresses, triple/fourth order moments - not all available at every location) | ||
| \(x=301\) mm | s301.dat | a301.dat |
| \(x=302\) mm | s302.dat | a302.dat |
| \(x=303\) mm | s303.dat | |
| \(x=304\) mm | s304.dat | a304.dat |
| \(x=305\) mm | s305.dat | a305.dat |
| \(x=306\) mm | s306.dat | |
| \(x=308\) mm | s308.dat | |
| \(x=310\) mm | s310.dat | a310.dat |
| \(x=315\) mm | s315.dat | |
| \(x=320\) mm | s320.dat | a320.dat |
| \(x=340\) mm | s340.dat | a340.dat |
| \(x=380\) mm | a380.dat | |
| \(x=400\) mm | s400.dat | |
| \(x=460\) mm | s460.dat | a460.dat |
| \(x=520\) mm | s520.dat | |
| \(x=580\) mm | s580.dat | a580.dat |
| \(x=1000\) mm | s1000.dat | a1000.dat |
| \(x=1240\) mm | a1240.dat | |
| \(x=1960\) mm | s1960.dat | a1960.dat |
| Profiles along the geometric centreline | ||
| Mean velocity, some 2nd/3rd/4th order moments | scl.dat | acl.dat |
| \(\partial U/\partial x\), maximum \(\partial U/\partial y\) | sstrain.dat | astrain.dat |
| Profiles of mean \(V\) velocity across the wake (symmetric wake Only) | |
|---|---|
| \(x=304\), \(305\), \(306\), \(308\), \(310\), \(312\), \(315\), \(320\), \(330\), \(340\) mm | symvs1.dat |
| \(x=520\), \(580\), \(680\) mm | symvs2.dat |
| \(x=760\), \(880\), \(1000\), \(1240\) mm | symvs3.dat |
| Profiles along domain outer edge (symmetric wake only) | |
| Static pressure | sstatp.dat |
| Streamlines (symmetric wake only) | |
| \((x,y)\) coordinates of streamlines for selected streamfunction \(\psi\) values | sstream.dat |
| Budgets (symmetric wake only) | |
|---|---|
| Readme file | balread-me.txt |
| \(k\) budget on centreline | skecl.dat |
| \(k\) budget at \(x=305\) mm | ske305.dat |
| \(k\) budget at \(x=340\) mm | ske340.dat |
| \(k\) budget at \(x=580\) mm | ske580.dat |
| \(k\) budget at \(x=1000\) mm | ske1000.dat |
| \(\overline{uv}\) budget at \(x=305\) mm | suv305.dat |
| \(\overline{uv}\) budget at \(x=340\) mm | suv340.dat |
| \(\overline{uv}\) budget at \(x=580\) mm | suv580.dat |
| \(\overline{uv}\) budget at \(x=1000\) mm | suv1000.dat |
| Spectra of \(u'\) - Asymmetric Wake | |||
|---|---|---|---|
| Readme file | aspec-read-me.txt | ||
| \(x=305\) mm | \(x=310\) mm | \(x=340\) mm | |
| \(y=0.0\) mm | 1asp305.dat | 1asp310.dat | 1asp340.dat |
| \(y=0.48\) mm | 2asp305.dat | 2asp310.dat | 2asp340.dat |
| \(y=1.0\) mm | 3asp305.dat | 3asp310.dat | 3asp340.dat |
| \(y=2.98\) mm | 4asp305.dat | 4asp310.dat | 4asp340.dat |
| \(y=6.98\) mm | 5asp305.dat | 5asp310.dat | 5asp340.dat |
| \(y=-0.0\) mm | 6asp305.dat | 6asp310.dat | 6asp340.dat |
| \(y=-0.5\) mm | 7asp305.dat | 7asp310.dat | 7asp340.dat |
| \(y=-1.0\) mm | 8asp305.dat | 8asp310.dat | 8asp340.dat |
| \(y=-3.0\) mm | 9asp305.dat | 9asp310.dat | 9asp340.dat |
| \(y=-7.0\) mm | 10asp305.dat | 10asp310.dat | 10asp340.dat |
References
- Erm, L.P., Joubert P.N. (1991). Low-Reynolds-number turbulent boundary layers. J. Fluid Mech., Vol. 230, pp. 1-44.
- Gough, T.D. (1996). Low Reynolds number turbulent boundary layers and wakes. PhD. Thesis, Dept. of Mechanical Engineering, University of Surrey.
- Gough, T.D., Hancock, P.E. (1996). Low Reynolds Number Turbulent Near Wakes. Advances in Turbulence VI. Fluid Mechanics and its Applications, Vol 36. (Eds. Gavrilakis S., Machiels L., Monkewitz P.A.), Springer.
- Hayakawa. M., Iida. S. (1992). Behavior of turbulence in the near wake of a thin flat plate at low Reynolds numbers, Phys. Fluids A, 4.2282-2291.
Indexed data:
| case035 (dbcase, free_flow) | |
|---|---|
| case | 035 |
| title | Low Reynolds Number Turbulent Flow Near Wakes |
| author | Gough, Hancock |
| year | 1986 |
| type | EXP |
| flow_tag | 2d, axisymmetric, wake |