Developing Flow in a Curved Rectangular Duct
Experiments by Kim and Patel
Description
The flow considered is a developing turbulent flow in a 90 deg. curved duct of rectangular cross-section. As shown in figure 1 there is an initial 2D wind tunnel constriction, resulting in a rectangular duct cross-section of width \(H=20.3\) cm and height \(6H\). Upstream of the bend there is a straight section of duct, of length \(7.5H\), and another straight section downstream of the bend, of length \(25.5H\). The bend itself has inner and outer radii of \(R_i=3H\) and \(R_o=4H\).
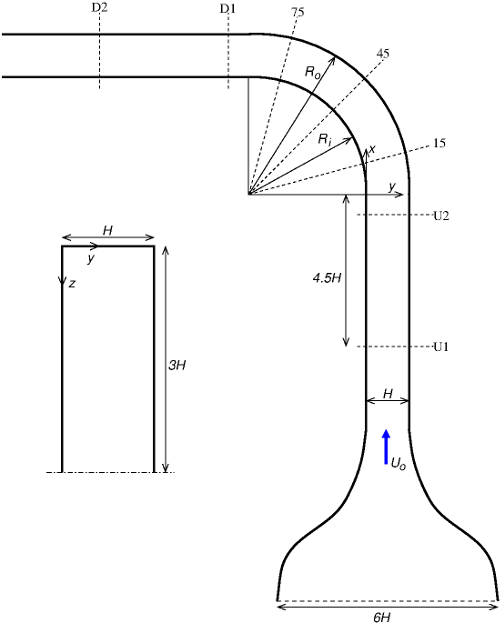 Fig. 1: Schematic of duct geometry
Fig. 1: Schematic of duct geometry
Measurements have been taken at two upstream locations (stations U1 and U2), three positions around the bend (15, 45 and 75) and two locations downstream of the bend (D1 and D2). Details are given in the table below.
| Measurement station | Location |
|---|---|
| U1 | \(4.5H\) upstream of the bend |
| U1 | \(0.5H\) upstream of the bend |
| 15 | \(15^o\) into the bend |
| 45 | \(45^o\) into the bend |
| 75 | \(75^o\) into the bend |
| D1 | \(0.5H\) downstream of the bend |
| D2 | \(4.5H\) downstream of the bend |
Flow Characteristics
The initially 2D boundary layers developing on the vertical lateral walls are subjected to strong streamwise curvatures and associated pressure gradients along the bend. On the other hand, the pressure-driven secondary motion in the corner regions eventually leads to the formation of a longitudinal vortex on the convex wall. The duct aspect ratio is such that these two features of the flow develop more or less independently, without interaction.
Flow Parameters
- Air with a kinematic viscosity: \(\nu = 1.45 \times 10^{-5}\) m2/s.
- Freestream velocity at station \(U1\) (\(x = -4.5H\)): \(U_o = 16\) m/s.
- Reynolds number: \(U_oH/\nu = 224,000\).
Inflow Conditions
At station U1 (\(x = -4.5H\)), the velocity is uniform in the core flow, outside the boundary layers, within a deviation less than 1%. On the vertical lateral walls, the boundary layers are of flat-plate type with a momentum thickness Reynolds number of 1650, a boundary layer thickness of \(\delta = 0.08H\) and a friction coefficient of \(C_f = 0.0038\). The 2D wind-tunnel contraction located \(3H\) upstream of U1 does introduce a secondary motion in the boundary layers on the top and bottom flat walls, but its magnitude reaches only 5% of the freestream velocity. Measurements are provided for what is the slightly three-dimensional duct flow at this location, which should in most cases be sufficiently detailed to be used as inlet conditions.
Experimental Details
Hot-wire velocity measurements have been carried out using a miniature X-wire probe for the turbulence quantities.
Mean velocity measurements have been carried out using a five-hole pressure probe with a diameter of 3 mm.
All velocity measurements have been made in the upper half of the duct divided into 5 different domains, namely in1, up1, ou1, in2, ou2 (see figure 2).
Wall shear stress, \(\tau_w\), measurements were made using two pressure probes in combination (only the magnitude is actually measured). The friction coefficient is defined as \(C_f = 2\tau_w/(\rho U_o^2)\).
Static pressure measurements were made using wall taps. The pressure coefficient is defined as \(C_p = 2(p - p_o)/(\rho U_o^2)\), where \(p_o\) is the static pressure at (\(0\),\(0\),\(3H\)).
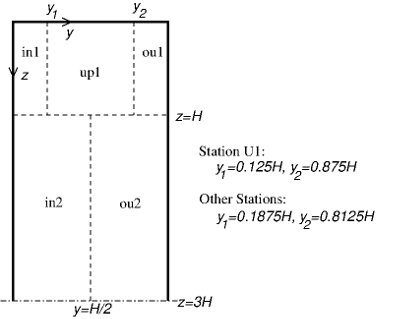 Fig. 2: Measurement domains across the upper half of the duct cross section
Fig. 2: Measurement domains across the upper half of the duct cross section
Measurement Errors
| \(\delta(U)\) | 1.5% |
| \(\delta(V)\), \(\delta(W)\) | 3% |
| \(\delta(\overline{u^2})\) | 5% |
| \(\delta(\text{other Reynolds stresses})\) | 10% |
Available Measurements
The measurements available include:
- Contour maps at selected streamwise locations (fice files per location, covering the five regions indicated in figure ##):
- Mean velocities \(U\), \(V\) and \(W\) at stations U1, U2, 15, 45, 75, D1, and D2
- Reynolds stresses \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\), \(\overline{uv}\), \(\overline{uw}\) at stations U1, U2, 45 and D1
- Profiles across the duct at a number of \(Z\) locations:
- Mean velocities \(U\), \(V\) and \(W\) at stations U1, U2, 15, 45, 75, D1, and D2
- Reynolds stresses \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\), \(\overline{uv}\), \(\overline{uw}\) at stations U1, U2, 45 and D1
- Wall pressure coefficient around the inner and outer walls of the duct, at duct mid-height
- Skin friction coefficient around the duct walls at measurement stations U1, U2, 15, 45, 75, D1 and D2
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
The file readme.txt has information on the data file naming and contents.
Pressure coefficients:
| pressure.dat | \(C_p\) around inner and outer duct walls |
| pressure-tab.dat | The same \(C_p\) data, but tabulated for different parts of inner/outer walls |
Skin friction:
| Station | Inner Wall | Top Wall | Outer Wall |
|---|---|---|---|
| U1 | su1in.dat | su1up.dat | su1out.dat |
| U2 | su2in.dat | su2up.dat | su2out.dat |
| 15 | s15in.dat | s15up.dat | s15out.dat |
| 45 | s45in.dat | s45up.dat | s45out.dat |
| 75 | s75in.dat | s75up.dat | s75out.dat |
| D1 | sd1in.dat | sd1up.dat | sd1out.dat |
| D2 | sd2in.dat | sd2up.dat | sd2out.dat |
Contour maps:
| in1 | up1 | ou1 | in2 | ou2 | |
|---|---|---|---|---|---|
| Mean velocities | |||||
| U1 | mu1in1.dat | mu1up1.dat | mu1ou1.dat | mu1in2.dat | mu1ou2.dat |
| U2 | mu2in1.dat | mu2up1.dat | mu2ou1.dat | mu2in2.dat | mu2ou2.dat |
| 15 | m15in1.dat | m15up1.dat | m15ou1.dat | m15in2.dat | m15ou2.dat |
| 45 | m45in1.dat | m45up1.dat | m45ou1.dat | m45in2.dat | m45ou2.dat |
| 75 | m75in1.dat | m75up1.dat | m75ou1.dat | m75in2.dat | m75ou2.dat |
| D1 | md1in1.dat | md1up1.dat | md1ou1.dat | md1in2.dat | md1ou2.dat |
| D2 | md2in1.dat | md2up1.dat | md2ou1.dat | md2in2.dat | md2ou2.dat |
| Reynolds stresses | |||||
| U1 | tu1in1.dat | tu1up1.dat | tu1ou1.dat | tu1in2.dat | tu1ou2.dat |
| U2 | tu2in1.dat | tu2up1.dat | tu2ou1.dat | tu2in2.dat | tu2ou2.dat |
| 45 | t45in1.dat | t45up1.dat | t45ou1.dat | t45in2.dat | t45ou2.dat |
| D1 | td1in1.dat | td1up1.dat | td1ou1.dat | td1in2.dat | td1ou2.dat |
Cross-Duct Profiles:
| Station | Mean Velocities | Reynolds Stresses |
|---|---|---|
| U1 | mu1sel.dat | tu1sel.dat |
| U2 | mu2sel.dat | tu2sel.dat |
| 15 | m15sel.dat | |
| 45 | m45sel.dat | t45sel.dat |
| 75 | m75sel.dat | |
| D1 | md1sel.dat | td1sel.dat |
| D2 | md2sel.dat |
Recommendations for calculations
Inlet conditions: The calculation of the duct flow can be started at station \(U1\) using the experimental values provided as inlet conditions. The non-measured quantity \(\overline{vw}\) may be assumed as negligible.
Symmetry: Due to geometric symmetry with respect to the \(z=0\) plane, one can use a computational domain including only the upper half of the duct.
Outlet conditions: The outlet should be placed sufficiently far downstream of the bend (\(x > 30H\)) so that zero gradients may be assumed for the flow variables.
Previous Numerical Studies
Sotiropoulos and Patel (1992) have performed calculations of this case with the two-layer \(k\)-\(\varepsilon\) model using two different numerical methods: the “finite-analytic” and a finite-difference method. In both cases, the overall structure of the flow was well predicted but both the strength of the secondary motion, and consequently its effect on the streamwise flow development, and the effects of wall curvature on the turbulence within the lateral boundary layers were underestimated.
Main References
- Kim, W.J., Patel, V.C. (1994). Origin and decay of longitudinal vortices in developing flow in a curved rectangular duct. J. Fluids Engineering, Vol. 116, pp. 45-52.
- Sotiropoulos, F., Patel, V.C. (1992). Flow in curved ducts of varying cross-section. IIHR Report No. 358, Institute of Hydraulic Research, University of Iowa.
Indexed data:
| case062 (dbcase, confined_flow) | |
|---|---|
| case | 062 |
| title | Developing flow in curved rectangular duct |
| author | Kim, Patel |
| year | 1991 |
| type | EXP |
| flow_tag | 3d, curvature, constant_cross_section |