Flat Plate Transitional Boundary Layer
LES by Yang and Voke
Description
The case consists of a flat-plate transitional 2D boundary layer flow without pressure gradient, and with no temperature variations.
Free-stream velocity: \(U_o=9.6\) m/s.
Upstream turbulence intensity: \(Tu_o=5.0\)%.
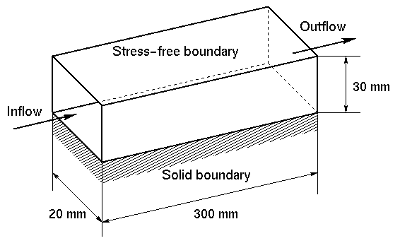
An LES has been performed using the geometry and boundary conditions shown schematically in figure 1.
Simulation Details
An LES was carried out using a finite volume based code, with a sub-grid-scale turbulent viscosity as described by Voke (1991) to account for low-Reynolds-number effects: \[ \nu_s = (\Delta c_s)^2 \sqrt{2s_{ij}s_{ij}} \qquad \nu_e = \nu_s - (2\nu/n)[ 1 - \exp(-n\nu_s/(2\nu)] \] with constants \(c_s=0.1\) \nd \(n=9\).
The LES was performed in a computational box extending from \(Re_x = 6620\) to \(200000\), or a total nominal length of 300 mm, equivalent to \(L_x^+ = 10138\) in wall units. The lateral and vertical dimensions of the box were \(L_z = 20\) mm (\(L_z^+ = 676\)) and \(L_y = 30\) mm (\(L_y^+ = 1014\)). The overall meshing was \(127 \times 56 \times 48\). These dimensions gave a resolution \(\Delta x^+ = 80\), \(\Delta z^+ = 14\), and \(\Delta y^+\) varying from 1 at the wall to 80 well beyond the boundary layer. The wall units are based on the friction velocity just after transition is complete.
The upstream boundary of the computation represented a point 10 mm downstream of the leading edge of the flat plate (\(Re_x=6620\)). An appropriate Blasius profile was imposed at the inflow boundary, with the free-stream disturbances limited to the region above \(y=0.3\) mm. There was a smooth cutoff of free-stream disturbances between \(y=0.3\) mm and \(y=0.65\) mm. The inflowing f.s.t. was derived from separate simulations on matched meshes but without any solid lower surface, and with pseudorandom disturbances at their inflow superimposed on a uniform flow. Velocity data were extracted from these simulations at \(x=150\) mm, \(50\) mm upstream of the outflow boundary of the simulations. These `precursor' simulations therefore mimicked the behaviour of grid turbulence, generating more realistic f.s.t. for input into the simulation of the boundary layer transition than a pseudorandom input would have done. The pseudorandom disturbances at the inflow of the precursor simulations decayed rapidly at first, but settled to a more physically realistic decay rate before they reached the \(x=150\) mm station at which velocity data were extracted for use as inflow to the boundary layer `successor' simulations.
Available data
The available data consists of:
- Profiles of mean \(U\) velocity, rms velocities \(u'\), \(v'\), \(w'\) and Reynolds shear stress \(\overline{uv}\) at \(x=25\), \(45\), \(95\) and \(195\) mm.
- Budgets of \(\overline{u^2}\), \(\overline{v^2}\), \(\overline{w^2}\) and \(\overline{uv}\) at the same four locations.
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Profiles (at the 4 \(x\) locations) | |
|---|---|
| \(U\) velocity | yv-t3b-meanu.dat |
| Rms \(u'\) | yv-t3b-uu.dat |
| Rms \(v'\) | yv-t3b-vv.dat |
| Rms \(w'\) | yv-t3b-ww.dat |
| Reynolds shear stress \(\overline{uv}\) | yv-t3b-uv.dat |
| Reynolds Stress Budgets | |
| \(\overline{u^2}\) budgets | yv-t3b-budguu.dat |
| \(\overline{v^2}\) budgets | yv-t3b-budgvv.dat |
| \(\overline{w^2}\) budgets | yv-t3b-budgww.dat |
| \(\overline{uv}\) budgets | yv-t3b-budguv.dat |
References
- Yang, Z.Y., Voke, P.R. (1993). Large-Eddy Simulation studies of bypass transition. Engineering Turbulence Modelling and Experiments 2, (Eds. W. Rodi et al), Elsevier Science, Amsterdam, pp. 603-611.
- Voke, P.R., Yang, Z.Y. (1993). Numerical studies of the mechanisms of bypass transition in the flat plate boundary layer. Proc. 9th Int. Symp. on Turbulent Shear Flows, Kyoto, Japan.
- Yang, Z.Y., Voke, P.R. (1993). Large-Eddy Simulation of transition under turbulence. Report ME-FD/93.12, Department of Mechanical Engineering, University of Surrey, U.K.
- Yang, Z.Y., Voke, P.R. (1993). Balance Equations in Finite-Volume Large-Eddy Simulations. Report ME-FD/94.27, Department of Mechanical Engineering, University of Surrey, U.K.
- Voke, P.R. (1993). Low-Reynolds-Number Subgrid-Scale Models. Report ME-FD/94.26, Department of Mechanical Engineering, University of Surrey, U.K.
Indexed data:
| case073 (dbcase, semi_confined_flow) | |
|---|---|
| case | 073 |
| title | Flat plate transitional boundary layer |
| author | Yang, Voke |
| year | 1995 |
| type | LES |
| flow_tag | 2d, transition, 2dbl |