Flow over Periodic Hills
LES by Temmerman and Leschziner
Flow Configuration
Flow over 2D periodic hills, consisting of polynomial-shaped obstacles mounted on a flat plate with a recirculation region in their wake, as shown in figure 1.
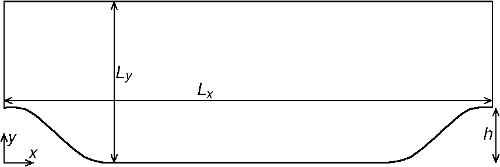 Fig. 1: Periodic hills geometry
Fig. 1: Periodic hills geometry
The test case is relevant for studying near-wall or/and subgrid-scale modelling in LES in the presence of separation and reattachment.
The geometry retains the shape of the hill defined by Almeida et al (1992) (see Case 18 of this database). As the true periodicity of the Almeida et al experiment (case 18-B) was in question during the 1995 ERCOFTAC/IAHR workshop when it was considered as one of the test cases, the present LES was set up to provide a fully periodic case.
The reference presented herein consists in a wall-resolving computation using the dynamic subgrid-scale model for a large-eddy simulation.
Geometrical Parameters
- Hill height: \(h = 28\) mm
- Hill crests are separated by: \(L_x = 9h\)
- Hill geometry is given as a series of spline functions, detailed in geom.dat
- Channel height: \(L_y = 3.035h\)
Flow Parameters
- Reynolds number: \(U_bh/\nu = 10 595\), based on the bulk velocity, \(U_b\), taken at the crest of the hill, and the hill height \(h\).
- The flow is periodic in the streamwise direction.
- The spanwise width of the LES computation is \(4.5h\).
Simulation details
The simulation was performed on a grid of approximately 5M nodes, covering a spanwise direction of 4.5 hill heights. The mesh was close to orthogonal, of low aspect ratio and mesh-expansion ratio below 1.05. The \(y^+\) value at the nodes closest to the wall was around 0.5, allowing the no-slip condition to be used directly. Statistical data was assembled over a period of 55 flow-through times, at a cost of approximately 50 000 processor hours on the Manchester CSAR Cray T3E computer.
Available LES Data
Separation is predicted at \(x=0.22h\) and reattachment at \(x=4.72h\). Typical mean streamlines are shown in figure 2.
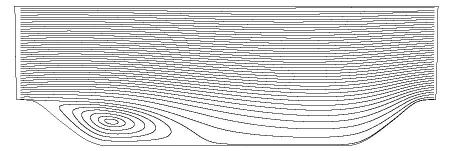 Fig. 2: Mean streamline pattern
Fig. 2: Mean streamline pattern
Profiles of the (\(U\)) and (\(V\)) mean velocities, Reynolds stresses \(\overline{u^2}\), \(\overline{v^2}\) and \(\overline{uv}\), and turbulent kinetic energy \(k\) are available at a number of \(x/h\) locations. All quantities are dimensionless (normalized using the bulk velocity, \(U_b\), and hill height, \(h\)).
Sample plots of selected quantities are available.
Compressed archive of the files can be downloaded from the link below, or files can be retrieved individually from the table.
| \(x/h\) Location | File |
|---|---|
| 0.05 | data-001.dat |
| 0.5 | data-002.dat |
| 1.0 | data-003.dat |
| 2.0 | data-004.dat |
| 3.0 | data-005.dat |
| 4.0 | data-006.dat |
| 5.0 | data-007.dat |
| 6.0 | data-008.dat |
| 7.0 | data-009.dat |
| 8.0 | data-010.dat |
Previous Numerical Solutions
Mellen et al. (2000) reported the first LES of this case. They, and later Temmerman et al. (2001), have performed a series of subgrid scale models and wall-treatment sensitivity tests, taking the LES results on a fine grid where no wall functions applied (data given herein) as a reference. The exact value of reattachment point was found to vary with SGS model and grid.
Some a priori tests can also be found in Jang et al. (2001).
Related Publications
- Almeida, G.P., Durao, D.F.G., Heitor, M.V. (1992). Wake flows behind two dimensional model hills. Exp. Thermal and Fluid Science, Vol. 7, p. 87.
- Jang, Y-J., Temmerman, L., Leschziner, M.A. (2001). Investigation of anisotropy-resolving turbulence models by reference to highly resolved LES data for separated flow, Proc. ECCOMAS Computational Fluid Dynamics Conference, Swansea.
- Mellen, C.P., Fröhlich, J., Rodi, W. (2000). Large Eddy Simulation of the flow over periodic hills, Proc. 16th IMACS World Congress, Lausanne.
- Temmerman, L., Leschziner, M.A. (2001). Large Eddy Simulation of separated flow in a streamwise periodic channel constriction, Proc. Int. Symp. on Turbulence and Shear Flow Phenomena, Stockholm.
Indexed data:
| case081 (dbcase, confined_flow) | |
|---|---|
| case | 081 |
| title | Flow over Periodic Hills |
| author | Temmerman, Leschziner |
| year | 2001 |
| type | LES |
| flow_tag | 2d, separated, varying_cross_section |