Couette Flow with Plane Fixed Wall
Direct Numerical Simulations by Kuroda, Kasagi, Hirata
Flow Description
Couette-Poiseuille flow in a channel, between a plane fixed wall and a plane moving wall. The mean shear rate on one wall is varied by changing the relative wall velocities and the streamwise pressure gradient, allowing the turbulence statistics and structures under different wall shear rates to be investigated.
Flow Characteristics
Schematic pictures of the type of flow simulated are shown in figure 1. The top wall is at rest, while the bottom wall is moving at a constant speed, \(U_w\).
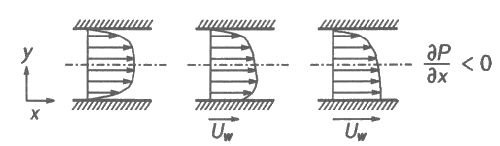 Fig. 1: Flow configuration schematics
Fig. 1: Flow configuration schematics
Data for the case of stationary lower wall (plane channel flow) is available elsewhere (including case032, case044 and case045 in this database). The parameters for the three cases reported here were chosen in order to give different shear stresses at the bottom wall (up to nearly the case of zero wall shear stress), whilst maintaining almost the same wall shear stress on the top wall.
The flow parameters and conditions for the three cases are summarized below:
- Air with a kinematic viscosity: \(\nu = 1.5 \times 10^{-5}\) m2/s
- Wall velocity: \(U_w\)
- Flow rate velocity: \(U_q\)
- Friction velocity on fixed wall: \(U_{\tau f}\)
- Friction velocity on moving wall: \(U_{\tau m}\)
- Channel half-width: \(\delta\)
- Non-dimensional pressure gradient: \(a = -(\delta/(\rho U_w^2)) \partial P/\partial x\)
| Case | \(U_w\delta/\nu\) | \(a\) | \(U_{\tau f}\delta/\nu\) | \(U_{\tau m}\delta/\nu\) |
| CP1 | 1800 | 0.00434 | 148 | 79.0 |
| CP2 | 2640 | 0.00186 | 152 | 49.0 |
| CP3 | 3000 | 0.00133 | 154 | 17.7 |
Simulation Details
Referring to the numerical procedure used by Kim et al. (1987), a fourth-order partial differential equation for \(v\), a second-order partial differential equation for the wall-normal component of vorticity \(\omega_y\) and the continuity equation were used to solve the flow field.
A spectral method with Fourier series in the \(x\) and \(z\) directions and a Chebyshev polynomial expansion in the wall-normal direction were used. The computational periods were chosen to be \(5\pi\delta\), \(2\delta\) and \(2\pi\delta\) in the \(x\), \(y\) and \(z\) directions, respectively. \(128 \times 128\) Fourier modes and Chebyshev polynomials up to the order 96 in wave number space were used in order to resolve all essential turbulent scales on the computation grid. The collocation grid used to compute the nonlinear terms in physical space had 1.5 times finer resolution in each direction to remove aliasing errors.
For time integration, the second-order Adams-Bashforth and Crank-Nicolson schemes were adopted for the nonlinear and viscous terms, respectively.
Data are non-dimensionalized by wall variables, i.e. \(U_{\tau f}\) and \(\nu\).
Available Data
The data available includes:
- Mean velocity and Reynolds stress profiles across the channel
- Skewness and flatness factors
- Budgets of Reynolds stresses, turbulent kinetic energy and its dissipation rate
- One dimensional energy spectra at selected \(y^+\) locations
- Two-point correlations at selected \(y^+\) locations
Sample plots of selected quantities are available.
The data can be downloaded as compressed archives from the links below, or as individual files.
| Case | Datafile |
| PC1 | pc12_pg_wl1.dat |
| PC2 | pc12_pg_wl2.dat |
| PC3 | pc12_pg_wl3.dat |
References
- Kim, J., Moin, P., Moser, R. (1987). Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech., Vol. 177, pp. 133-166.
- Kuroda, A., Kasagi, N., Hirata, M. (1993). A direct numerical simulation of turbulent plane Couette-Poiseuille flows: effect of near stream on the near wall turbulence structures. Proc. 9th Turbulent Shear Flows Symposium, Kyoto, Japan.
- Kuroda, A. (1990). Direct numerical simulation of Couette-Poiseuille flows. Dr. Eng. Thesis, the University of Tokyo.
Indexed data:
| case046 (dbcase, confined_flow) | |
|---|---|
| case | 046 |
| title | Couette Flow with Plane Fixed Wall |
| author | Kuroda, Kasagi, Hirata |
| year | 1993 |
| type | DNS |
| flow_tag | constant_cross_section, channel_flow |